Simple and weighted arithmetic average

The Arithmetic Mean of a dataset is obtained by summing all values ​​and dividing the found value by the number of datasets in that set.

It is widely used in statistics as a measure of central tendency.

It can be simple, where all values ​​have the same importance, or weighted, when considering different weights to the data.

Simple Arithmetic Average

This type of average works best when the values ​​are relatively uniform.

As it is sensitive to data, it does not always provide the most suitable results.

This is because all data have the same importance (weight).

Formula

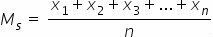
Where,

M_s: simple arithmetic mean
x₁, x₂, x₃,...,x_no: data values
n: number of data

Example:

Knowing that a student's grades were: 8.2; 7,8; 10,0; 9,5; 6,7, what is the average he obtained in the course?

Weighted Arithmetic Average

The weighted arithmetic mean is calculated by multiplying each value in the dataset by its weight.

Then find the sum of these values ​​which will be divided by the sum of the weights.

Formula

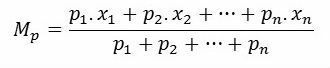
Where,

M_P: weighted arithmetic mean
P₁, P₂,..., P_no: weights
x₁, x₂,...,x_no: data values

Example:

Considering the grades and the respective weights of each one of them, indicate the average that the student obtained in the course.

subject	Note	Weight
Biology	8,2	3
Philosophy	10,0	2
Physics	9,5	4
geography	7,8	2
History	10,0	2
Portuguese language	9,5	3
Math	6,7	4

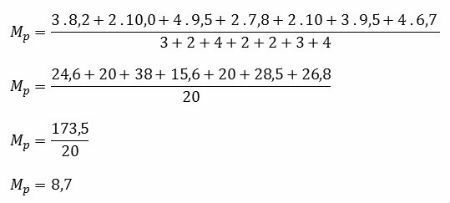
Read:

• Geometric Mean
• Average, Fashion and Median
• Variance and Standard Deviation

Commented Enem Exercises

1. (ENEM-2012) The table below shows the evolution of annual gross revenue in the last three years of five micro-enterprises (ME) that are for sale.

ME	2009 (in thousands of reais)	2010 (in thousands of reais)	2011 (in thousands of reais)
Pins V	200	220	240
W bullets	200	230	200
Chocolates X	250	210	215
Pizzeria Y	230	230	230
Weaving Z	160	210	245

An investor wants to buy two of the companies listed in the table. To do so, it calculates the average annual gross revenue for the last three years (from 2009 to 2011) and chooses the two companies with the highest annual average.

The companies that this investor chooses to buy are:

a) Candy W and Pizzeria Y.
b) Chocolates X and Weaving Z.
c) Pizzeria Y and Pins V.
d) Pizzeria Y and Chocolates X.
e) Weaving Z and Pins V.

See Answer

Average of Pins V = (200 + 220 + 240) / 3 = 220
Average of Bullets W = (200 + 230 + 200) / 3 = 210
Average of Chocolates X = (250 + 210 + 215) / 3 = 225
Average Pizzeria Y = (230 + 230 + 230) / 3 = 230
Average of P Weaving Z = (160 + 210 + 245) / 3 = 205

The two companies with the highest average annual gross revenue are Pizzeria Y and Chocolates X, with 230 and 225 respectively.

Alternative d: Pizzeria Y and Chocolates X.

2. (ENEM-2014) At the end of a science competition at a school, only three candidates remained.

According to the rules, the winner will be the candidate who obtains the highest weighted average between the grades of the final exams in chemistry and physics, considering, respectively, the weights 4 and 6 for them. Notes are always whole numbers.

For medical reasons, candidate II has not yet taken the final chemistry exam. On the day your assessment is applied, the grades of the other two candidates, in both subjects, will have already been released.

The table shows the grades obtained by the finalists in the final exams.

Candidate	Chemistry	Physics
I	20	23
II	x	25
III	21	18

The lowest grade that candidate II must obtain in the final chemistry test to win the competition is:

a) 18
b) 19
c) 22
d) 25
e) 26

See Answer

Candidate I
Weighted Average (MP) = (20 * 4 + 23 * 6) / 10
MP = (80 + 138) / 10
MP = 22

Candidate III
Weighted Average (MP) = (21 * 4 + 18 * 6) / 10
MP = (84 + 108) / 10
MP = 19

Candidate II
Weighted Average (MP) = (x * 4 + 25 * 6) / 10 > 22
MP = (x * 4 + 25 * 6) / 10 = 22
4x + 150 = 220
4x = 70
x = 70 / 4
X = 17.5

Thus, as the grades are always whole numbers, the lowest grade that candidate II must obtain in the final chemistry test to win the competition is 18.

Alternative to: 18.

See too:

• Statistic
• Statistics - Exercises
• Standard deviation
• Dispersion Measures