Fractions represent parts of a whole. From them, addition, subtraction, multiplication and division operations can be performed.
Addition and Subtraction of Fractions is done by adding or subtracting the numerators, depending on the operation. As for the denominators, as long as they are equal, they keep the same basis.
Remember that in fractions, the upper term is the numerator and the lower term is the denominator.
Examples:
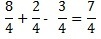
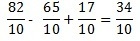
And when the denominators are different?
When the denominators are different, they must be equalized. This is done from the least common multiple (MMC), which is nothing more than the smallest number capable of dividing another number.
Example1:
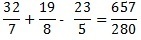
The MMC is 280 why?
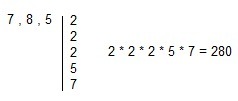
After finding the MMC of 7, 8 and 5, we have to divide it by the denominator and multiply by the numerator. Thus: 280 /7 = 40 and 40*32 = 1280. In turn, 280 /8 = 35 and 35*19 = 665, as well as 280/5 = 56 and 56*23 = 1288.

Example2:
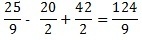
The MMC is 18 why?
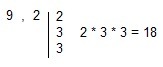
After finding the MMC of 9 and 2, we have to divide it by the denominator and multiply by the numerator. Thus: 18/9 = 2 and 2*25 = 50. In turn, 18/2 = 9 and 9*20 = 180, as well as 18/2 =9 and 9*42 = 378
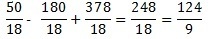
In this last example, we simplify the fraction, which means we reduce it by its common divisor. So we make the fraction simpler by dividing the numerator and denominator by the same number: 248/2 = 124 and 18/2 = 9.
Commented exercises on addition and subtraction of fractions
question 1
Perform operations with the following fractions and simplify the result when necessary.
The)
Right answer: .
(we have the sum of fractions with different denominators).
The first step to solve this operation is to make the fractions have the same denominator.
In this case, we can multiply the first fraction by 2 so that the denominator of the fraction is the number 8.
So we have the equivalent fraction of é
. Now we can add the second fraction.
Therefore, the sum of with
gives us the result of
.
B)
Right answer: .
(we have the subtraction of fractions with different denominators).
Initially, we need to transform the given fractions into equivalent fractions with the same denominator.
Now we can subtract the fractions and find the result.
Note that the found fraction can be simplified, as 14 and 24 have a common divisor, which is the number 2.
Therefore, the subtraction of per
give us the result
.
ç)
Right answer: .
(We have addition and subtraction of fractions with equal denominators).
To solve the operations with fractions, we must repeat the denominator, add and subtract the numerators.
So, adding up with
we have the fraction
and subtracting
of this result, we find the final answer, which is
.
question 2
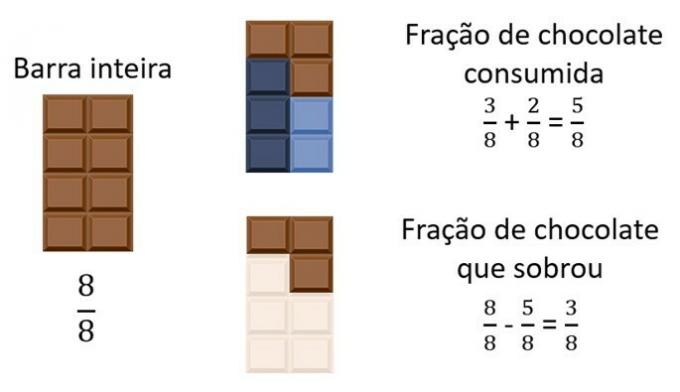
I bought a candy bar that had a total of eight squares. I ate three squares of chocolate yesterday and two squares of chocolate today. What fraction of chocolate have I already eaten? And what fraction is still left to eat?
a) I ate 5/8 and left 3/8.
b) I ate 6/8 and left 2/8.
c) I ate 3/8 and left 5/8.
Correct answer: a) I ate and left over
.
As the chocolate was divided into eight small squares, so the fraction representing the entire bar is .
Yesterday I ate three squares of chocolate out of a total of 8. So the fraction I ate yesterday is .
Today I ate two squares. Remember: a fraction represents a part of a whole. Therefore, the denominator must be the complete bar, that is, 8 small squares. So today I ate .
To know the fraction that represents the amount of chocolate consumed, we must add fractions.
In this case, we have addition with equal denominators.
The amount of chocolate left over can be calculated by subtracting fractions.
For this, we subtract from the total fraction the amount that was consumed.
We saw that to add or subtract fractions with equal denominators we must keep the denominator and subtract or add the numerators.
Therefore, the fraction of chocolate consumed is and the amount left is
.
Note in the image below how fractions are represented.
question 3
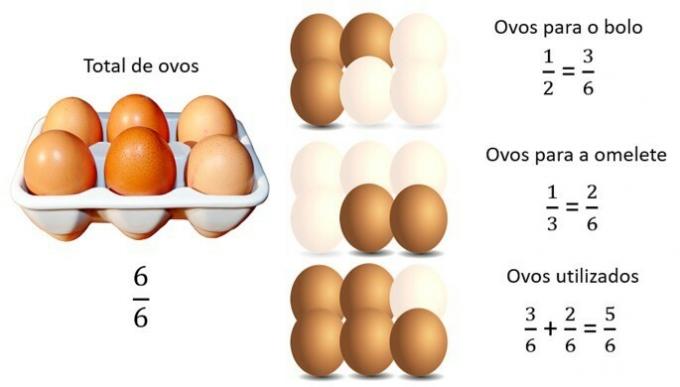
Ana has a box with 6 eggs. She plans to use them to make two recipes. For a cake, you need to use half the eggs and to make an omelet you need to use a third of the eggs. How many eggs did Ana use to make the two recipes?
a) 4 eggs
b) 5 eggs
c) 6 eggs
Correct answer: b) 5 eggs.
The fractions described in the question for the recipes are: from eggs to the cake and
of eggs for the omelet.
To find the total number of eggs used, we must add the fractions: .
However, since fractions have different denominators, we must initially transform the given fractions into fractions with similar denominators.
Adding up the equivalent fractions, we have:
The fraction denominator represents the whole and the numerator is the part used. Therefore, to make the two recipes, Ana used 5 eggs.
See the image below how fractions are represented.
Complement your studies on the subject by reading the texts below:
- What is fraction?
- Types of fractions and fractional operations
- Multiplication and Division of Fractions
- Equivalent Fractions
- generating fraction
- Fraction Exercises
If you are looking for a text with an approach to early childhood education, read: Operation with fractions - Kids and Fractions - Kids.

