THE Percentage or Percentage represents a ratio whose denominator equals 100 and indicates a part-to-whole comparison.
The % symbol is used to designate the percentage. A percentage value can also be expressed as a centesimal fraction (denominator equal to 100) or as a decimal number.
Example:
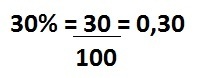
For easier understanding, see the table below:
| Percentage | Centesimal Ratio | Decimal Number |
|---|---|---|
| 1% | 1/100 | 0,01 |
| 5% | 5/100 | 0,05 |
| 10% | 10/100 | 0,1 |
| 120% | 120/100 | 1,2 |
| 250% | 250/100 | 2,5 |
Learn more about fractions and the Decimal numbers.
How to Calculate Percentage?
We can use several ways to calculate the percentage. Below we present three different ways:
- rule of three
- transformation of percentage into fraction with denominator equal to 100
- percentage transformation into decimal number
We must choose the most suitable way according to the problem we want to solve.
Examples:
1) Calculate 30% of 90
To use the rule of three in the problem, let's assume that 90 corresponds to the whole, ie 100%. The value we want to find will be called x. The rule of three will be expressed as:

To solve using fractions, we first have to turn the percentage into a fraction with a denominator equal to 100:
We can also transform the percentage into a decimal number:
30% = 0,3
0,3. 90 = 27
The result is the same in all three forms, that is, 30% of 90 corresponds to 27.
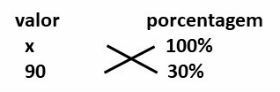
2) 90 corresponds to 30% of what value?
Note that in this example, we already know the percentage result and we want to know the value that corresponds to the whole (100%).
Using the rule of three, we have:
We can still solve the problem by transforming the percentage into a decimal number:
30% = 0,3
So just solve the following equation:
So 30% of 300 equals 90.
3) 90 corresponds to how much percent of 360?
We can solve this problem by writing in the form of a fraction:
Or, we can solve it using rule of three:
Thus, 90 corresponds to 25% of 360.
See too: how to calculate percentage?
Solved Exercises
To test your knowledge of the topic, below are exercises on calculating the percentage:
1. Calculate the values below:
a) 6% of 100
b) 70% of 100
c) 30% of 50
d) 20% of 60
e) 25% of 200
f) 7.5% of 400
g) 42% of 300
h) 10% of 62.5
i) 0.1% of 350
j) 0.5% of 6000
a) 6% of 100 = 6
b) 70% of 100 = 70
c) 30% of 50 = 15
d) 20% of 60 = 12
e) 25% of 200 = 50
f) 7.5% of 400 = 30
g) 42% of 300 = 126
h) 10% of 62.5 = 6.25
i) 0.1% of 350 = 0.35
j) 0.5% of 6000 = 30
How about knowing: What is Inflation?
2. (ENEM 2013)
To increase sales at the beginning of the year, a department store re-priced its products 20% below the original price. When they arrive at the checkout, customers who have the store's loyalty card are entitled to an additional 10% discount on the total value of their purchases.
A customer wants to buy a product that cost R$50.00 before the price markdown. He does not have the store's loyalty card. If this customer had the store's loyalty card, the additional savings they would obtain when making the purchase, in reais, would be:
a) 15.00
b) 14.00
c) 10.00
d) 5.00
e) 4.00
First of all, you should read the exercise carefully and note the values that are given:
Original value of the product: R$50.00.
Prices have 20% discount.
Soon:
Applying the price discount, we have:
50. 0,2 = 10
The initial discount will be R$10.00. Calculating on the original value of the product: R$50.00 - R$10.00 = R$40.00.
If the person has a loyalty card, the discount will be even greater, that is, the customer will pay R$40.00 with another 10% discount. Thus,
Applying the new discount:
40. 0,1 = 4
Therefore, the additional savings discount for those who have the loyalty card will be more BRL 4.00.
Alternative e: 4.00
Simple and Compound Interest
The interest system (simple or compound) represents concepts that are associated with percentage and commercial and financial mathematics.
O simple swear corresponds to the value added (through a percentage rate) over time; it's the compound interest basically consists of interest charged on interest. Remember that the percentage concept is often used to calculate interest, discounts and profits.
Ratio and Proportion
THE reason and proportion these are two concepts in mathematics that contribute to the understanding of various calculations, be it the rule of three or the percentage.
The reason is the relative comparison between two quantities. It represents the quotient between two numbers that is found by dividing and multiplying, for example, 12:6 = 2 (the ratio of 12 to 6 equals 2).
The proportion is the equality of two ratios, for example: 2.3=1.6 (thus, a.b=c.d) with the value of 6=6.
know more:
- Compound Interest Exercises
- Simple and Compound Three Rule
- Rule of Three Exercises
- Financial math
- Simple Interest Exercises
- Mathematics in Enem
- Math Formulas