At 2nd degree inequalities or quadratic inequalities differ from 2nd degree equations just for presenting a inequality in place of the equal sign of the equations. The way to determine the solution of quadratic inequalities is very similar to the process of identifying the roots of a 2nd degree equation. The distinction appears in determining the solution to the inequality, as it is necessary to analyze its sign.
Let's look at some examples of quadratic inequalities to comment on possible resolution processes.
Example 1: x² + x – 2 > 0
The same way we would solve a 2nd degree equation equal to x² + x – 2 = 0, we will use the Bhaskara formula to resolve this inequality:

Δ = b² - 4.a.c
Δ= 1² – 4.1.(– 2)
Δ= 1 + 8
Δ= 9
x = – b ± √Δ
2nd
x = – 1 ± √9
2.1
x = – 1 ± 3
2
x1 = – 1 + 3 = 2 = 1
2 2
x2 = – 1 – 3 = – 4 = – 2
2 2
The solutions found, x1 = 1 and x2 = – 2, are values for which the inequality is equal to zero. But looking closely, the inequality x² + x – 2 > 0 look for values that are bigger that zero. In this case, let's analyze the variation of the signal of
x² + x – 2 > 0, remembering that your graph is an upward-facing concavity. See the study of the sign of this inequality:Do not stop now... There's more after the advertising ;)
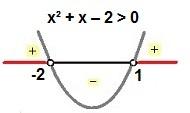
Study of the sign of the inequality x² + x – 2 > 0
In this case, the solution is 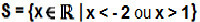 .
.
Example 2: x² - 4x ≤ 0
This example offers an incomplete inequality. So how can we solve a incomplete high school equation without using Bhaskara's formula, we will solve the inequality more simply. First let's put the x in evidence:
x² - 4x = 0
x.(x – 4) = 0
x1 = 0
x2 – 4 = 0
x2 = 4
There are two solutions: x1 = 0 and x2 = 4. Note that inequality looks for values less than or equal to zero, then x1 = 0 and x2 = 4 will be part of the solution. See the study of the sign of this inequality:
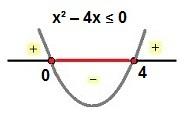
Study of the sign of the inequality x² – 4x ≤ 0
So the solution is 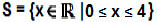 .
.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Second Degree Inequalities"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/inequacoes-2-grau.htm. Accessed on June 29, 2021.
Inequation, what is inequality, signs of inequality, study of the sign, study of the sign of an inequality, product inequality, product of inequalities, function, sign game.
