Circumference is flat figure built by set of points that are the same distance from the center. Known as elements of the circle, we call the point at the center the center or origin; of radius, the line segment that connects the center to the circumference; of rope, any segment that connects two ends of the circumference; and in diameter, any string that passes through the center. The length and area of the circle are calculated by specific formulas.
See too: Rectangle triangle - flat figure that has one of 90º between its three angles
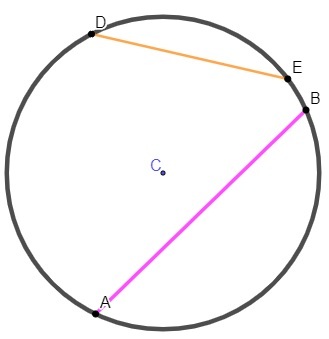
elements of the circle
To construct a circle, we need a point known as the center or origin and a specified distance known as the radius. The circle is formed by all the points that are at the same distance r of center. Note that the center is not part of the circle, but is the reference for its construction.
Having a good understanding of the construction of the circle, we can define its elements, which are the center, radius, chord and diameter.
Center and radius:
fundamental for the construction of the circle, as the name suggests, center is a point that is the same distance from the circle. already the lightning, denoted by r, it is any segment of a straight line that starts from the center and goes to the circumference. the distance r it is of great importance to calculate the area and length of this figure.

C → center
r → radius
Rope and diameter: rope is any straight segment which has both ends on the circumference. The diameter is a string that passes through the center of the circumference, being the longest string in this figure.

The length of the diameter is always equal to twice the radius.
d = 2r |
Difference between circle and circumference
Many people think that circumference and circle are the same thing, but that's not quite the case. As we have seen, circumference is the set of points that are at the same distance from the center, since the circle is the region bounded by the circumference. Directly, circumference is the “contour”, and circle is the inner region of the figure.


See too: Difference between circumference, circle and sphere
circumference length
This is the same idea as when calculating the perimeter of a polygon. The length of the circle is calculated by:
C = 2·π·r |
Ç →length
r → radius
π → (reads: pi)
O π is a Greek letter that we use to represent a constant and is useful for calculations with the circle. As π is an irrational number (π = 3.141592653589793238...), to do the math, we make an approximation of it.
In questions regarding entrance exams, Enem and competition, this value is given in the statement, the most adopted is 3.14, but there are questions that use 3.1 or even 3 as a value of π.
Example
Calculate the length of the circle that has a radius equal to 4 cm (use π = 3.1):
C = 2 πr
C = 2 · 3.1 · 4
C = 6.2 · 4
C = 24.8 cm
Example 2
Calculate the length of the circumference below knowing that its diameter is given in cm.
(Use π = 3.14)

If d = 12 cm, then the radius is half the diameter, r = 6.
C = 2 πr
C = 2 · 3.14 · 6
C = 6.28 · 6
C = 37.68 cm
circle area
The area of a circle is calculated using the formula:
A=π·r² |
A → area
r → radius
π → (reads: pi)
Example
What is the area of the circle in the following image? (π = 3)

r = 8 and π = 3
A = π · r²
A = 3 · 8²
A = 3 · 64
H = 192 cm²
Example 2
Calculate the area of a circle bounded by a circumference with a diameter equal to 10 cm.
If the diameter is 10 cm, the radius will be 5 cm.
Since the question gave us no value for π, we will not substitute any value in its place.
A = π · r²
A = π · 5²
A = 25 π cm²
See too:Cone – geometric solid whose base is formed by a circle

solved exercises
question 1 - A cyclist is riding through a square in a circular shape with a diameter of 15 m. Knowing that, at the end of training, he completed 150 laps, the amount of km covered was: (Use π = 3)
a) 13.5 km
b) 135 km
c) 22.5 km
d) 250 km
Resolution
Alternative A.
1st step: calculate the circumference length:
C = 2 πr
C = 2 · 3 · 15
C = 6 · 15
C = 90 m
2nd step: multiply the last result by the number of laps given:
90 · 150 = 13,500 m
3rd step: convert meters to kilometers (just divide by 1000)
13,500: 1000 = 13.5 km
Question 2 - A manhole cover broke, and another had to be made. In order for it to be perfect, it needs to have the same area as the previous lid. For this, the sanitation company measured the radius of the previous cover as shown in the following figure:

The lid area is the same as:
(Use π = 3.14)
a) 780.5 cm²
b) 1875 cm²
c) 625 cm²
d) 1962.5 cm²
Resolution
Alternative D.
A = π · r²
A = 3.14 · 25²
A = 3.14 · 625
A = 1962.5 cm²