Inequality of 1st and 2nd Degrees: how to solve and exercises

Inequation is a mathematical sentence that has at least one unknown value (unknown) and represents an inequality.

In the inequalities we use the symbols:

• > greater than
• ≥ greater than or equal
• ≤ less than or equal

Examples

a) 3x - 5 > 62
b) 10 + 2x ≤ 20

First Degree Inequality

An inequality is of the 1st degree when the largest exponent of the unknown is equal to 1. They can take the following forms:

• ax + b >0
• ax + b
• ax + b ≥ 0
• ax + b ≤ 0

Being The and B real numbers and The ≠ 0

Resolution of a first degree inequality.

To solve such an inequality, we can do it the same way we do in equations.

However, we must be careful when the unknown becomes negative.

In this case, we must multiply by (-1) and invert the inequality symbol.

Examples

a) Solve the inequality 3x + 19

To solve the inequality we must isolate the x, passing the 19 and the 3 to the other side of the inequality.

Remembering that when changing sides we must change the operation. Thus, the 19 that was adding will pass decreasing and the 3 that was multiplying will pass dividing.

3xxx

b) How to solve the inequality 15 - 7x ≥ 2x - 30?

When there are algebraic terms (x) on both sides of the inequality, we must join them on the same side.
By doing this, the numbers that change sides have their sign changed.

15 - 7x ≥ 2x - 30
- 7x - 2x ≥ - 30 -15
- 9x ≥ - 45

Now, let's multiply the entire inequality by (-1). To do so, we change the sign of all terms:

9x ≤ 45 (note that we invert the symbol ≥ to ≤)
x ≤ 45/9
x ≤ 5

Therefore, the solution to this inequality is x ≤ 5.

Resolution using the inequality graph

Another way to solve an inequality is to graph it on the Cartesian plane.

In the graph, we study the sign of inequality by identifying which values ​​of x turn inequality into a true sentence.

To solve an inequality using this method we must follow the steps:

1st) Put all the terms of the inequality on the same side.
2º) Replace the sign of inequality with that of equality.
3rd) Solve the equation, that is, find its root.
4th) Study the sign of the equation, identifying the values ​​of x that represent the solution of inequality.

Example

Solve the inequality 3x + 19

First, let's write the inequality with all the terms on one side of the inequality:

3x + 19 - 40 3x - 21

This expression indicates that the solution of the inequality is the values ​​of x that make the inequality negative (

Find the root of the equation 3x - 21 = 0

x = 21/3
x = 7 (root of the equation)

Represent in the Cartesian plane the pairs of points found when substituting values ​​in the x in the equation. The graph of this type of equation is a straight.

We identified that the values

Second Degree Inequality

An inequality is of the 2nd degree when the largest exponent of the unknown is equal to 2. They can take the following forms:

• ax² + bx + c > 0
• ax² + bx + c
• ax² + bx + c ≥ 0
• ax² + bx + c ≤ 0

Being The, B and ç real numbers and The ≠ 0

We can solve this type of inequality using the graph representing the 2nd degree equation to study the sign, just as we did for the 1st degree inequality.

Remembering that, in this case, the graphic will be a parable.

Example

Solve inequality x² - 4x - 4

To solve a second degree inequality, it is necessary to find values ​​whose expression on the left side of the sign

First, identify the coefficients:

a = 1
b = - 1
c = - 6

We use the Bhaskara formula (Δ = b² - 4ac) and we substitute the values ​​of the coefficients:

Δ = (- 1)² - 4. 1. (- 6)
Δ = 1 + 24
Δ = 25

Continuing with Bhaskara's formula, we replaced again by the values ​​of our coefficients:

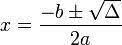
x = (1 ± √25) / 2
x = (1 ± 5) / 2

x₁ = (1 + 5)/ 2
x₁ = 6 / 2
x₁ = 3

x₂ = (1 - 5) / 2
x₁ = - 4 / 2
x₁ = - 2

The roots of the equation are -2 and 3. as the Theof the 2nd degree equation is positive, its graph will have the concavity facing up.

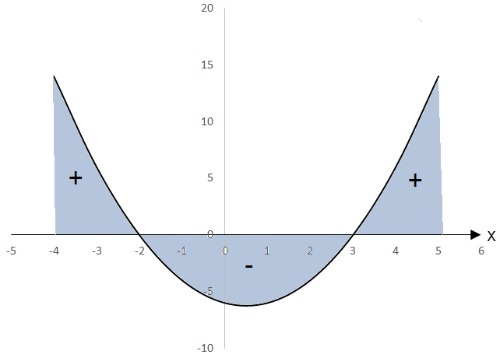
From the graph, we observe that the values ​​that satisfy the inequality are: - 2

We can indicate the solution using the following notation:

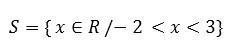
Read too:

• First Degree Equation
• Second degree equation
• Equation Systems

Exercises

1. (FUVEST 2008) By medical recommendation, a person must, for a short period, follow a diet that guarantees a daily minimum of 7 milligrams of vitamin A and 60 micrograms of vitamin D, feeding exclusively on a special yogurt and a mixture of cereals, accommodated in packages.

Each liter of yogurt provides 1 milligram of vitamin A and 20 micrograms of vitamin D. Each packet of cereal provides 3 milligrams of vitamin A and 15 micrograms of vitamin D.

By consuming x liters of yogurt and y packets of cereals daily, the person will be sure to be following the diet if:

a) x + 3y ≥ 7 and 20x + 15y ≥ 60
b) x + 3y ≤ 7 and 20x + 15y ≤ 60
c) x + 20y ≥ 7 and 3x + 15y ≥ 60
d) x + 20y ≤ 7 and 3x + 15y ≤ 60
e) x + 15y ≥ 7 and 3x + 20y ≥ 60

See Answer

Alternative to: x + 3y ≥ 7 and 20x + 15y ≥ 60

2. (UFC 2002) A city is served by two telephone companies. Company X charges a monthly subscription of R$35.00 plus R$0.50 per minute used. Company Y charges, per month, a subscription of R$26.00 plus R$0.50 per minute used. After how many minutes of use will company X's plan be more beneficial to customers than company Y's plan?

See Answer

26 + 0.65 m > 35 + 0.5 m
0.65 m - 0.5 m > 35 - 26
0.15 m > 9
m > 9/0.15
m > 60

From 60 minutes onwards, the company X plan is more advantageous.