At trigonometric functionsare the functions sine, cosine and tangent. All trigonometric functions relate the value of angle in degrees or radians with the value of the trigonometric ratio, a relationship that can be done through the study of the trigonometric cycle. With the individual study of each of the trigonometric functions, it is possible to make the representation graph, study the sign of the function for each of the quadrants, among other features important.
Read too: The 4 most made mistakes in tbasic rigidity
What are trigonometric functions?
The most common trigonometric functions are the sine function, the cosine function and the tangent function. Their study is linked to the trigonometric cycle.

For each angle value, there is a unique sine and cosine value. Trigonometric functions are nothing but the relationship between the angle and the value of the trigonometric ratio for that angle. Remember that the value of this angle can be given in radians or degrees and that the value of sine and cosine is always a real number between -1 and 1.
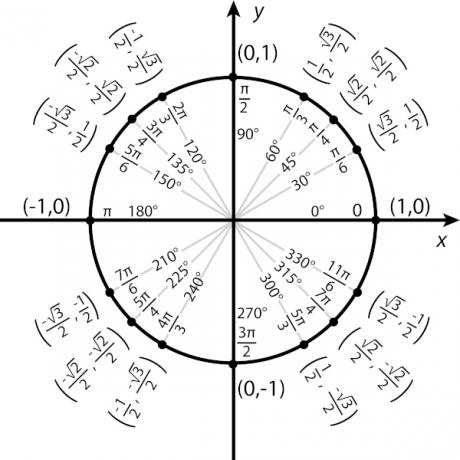
Note in the image that, for each angle, the cosine and sine admitm a value. It is based on the study of each of the trigonometric functions that we observe the relationship between the angle value and the trigonometric ratio value.
Read too: What are the remarkable angles?
Do not stop now... There's more after the advertising ;)
cosine function
The cosine function is the function f: R → R, whose formation law is f(x) = cos(x). As the cosine of an angle is always a number between 1 and -1, then -1 ≤ cos (x) ≤ 1.
Domain
The domain of the cosine function is the set of real numbers, because there is no restriction on the value of x, where x is the angle in radians. For every real number, you can find the value of cos(x), so Df= A.
Image
We know that the counterdomain of the cosine function is the set of real numbers, however, when we analyze the image of the function, it is possible to see that it is always a value greater than or equal to -1 and less than or equal to 1, since the trigonometric cycle has radius 1, so the largest value the cosine function can take is 1, and, similarly, the smallest value it can take is -1. Im = [-1, 1]
Cosine function graph
The graph of the cosine function iscontained in between the straightsy = -1 and y = 1. Remember that this happens because the image of the function is always a number between -1 and 1 and has an increasing part and decreasing part, as we can see below:

By matching the angle value with the trigonometric ratio value, you can see that the graphic has a cyclical behavior, that is, the behavior always repeats itself periodically. The graph of the cosine function is known as the cosine.
Signal
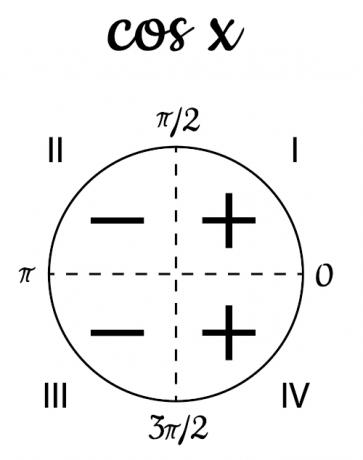
We know that, in the trigonometric cycle, the cosine has positive valuesin the I and IV quadrants. The first quadrant is between 0º and 90º, and the fourth quadrant is between 270º and 360º. In radians, the function is positive for values of x between 0 and π/2 and between 3π/2 and 2π.
The cosine function has negative valuesin the II and III quadrants, that is, the angle is between 90º and 270º. In radians, for the cosine function to be negative, x is between π/2 and 3π/2.
Cosine function period
The graph of the cosine function has a 2π period. Analyzing, it is possible to see that the graph is contained in the range from 0 to 2π. For values before or after this range, the graph repeats.
Parity
The cosine function is considered a even function, as there is symmetry in the graph with respect to the y axis. When a function is considered even, we have to f (x) = f (-x), that is, cos (x) = cos (-x).
Remarkable arcs of the cosine function
Let's look at the cosine value for the main angles:

See too: Secant, cosecant and cotangent - inverse trigonometric ratios of sine, cosine and tangent
sine function
The cosine function is the function f: R → R, whose formation law is f(x) = sin(x). Like the sine of an angle, just like the cosine, is always a number between 1 and -1, then -1 ≤ sin (x) ≤ 1.
Domain
The domain of the sine function is the set of real numbers. The function f(x) = sin (x) is defined for all real numbers, so Df= A.
Image
The sine function image has maximum value in f(x) = 1 and minimum value whenf(x) = -1. So the image of the function is the real range [-1, 1].
sine function graph
The graph of the sine function it is also limited by the horizontal lines y = -1 and y = 1. The behavior is similar to that of the periodic sine function, having increasing intervals and decreasing intervals. See the graphic representation of the sine function in the Cartesian plane below:
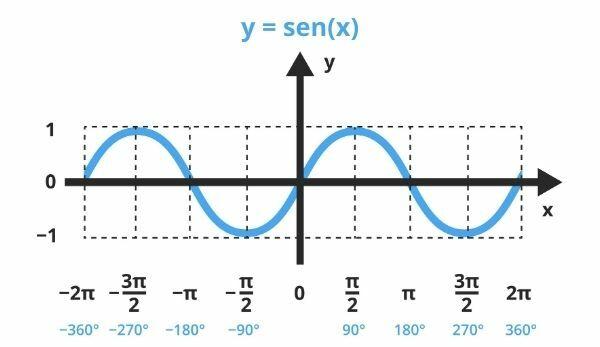
The graph of the sine function is also periodic and is known as a sine.
Signal
Unlike the cosine function, the sine function has positive values ins quadrants I and II first, that is, for angles between 0° and 180°. In radians, the function is positive for values between 0 and π.
The sine function has negative valuesin III and IV quadrants, that is, the angle is between 180º and 360º. In radians, for the sine function to be negative, x is between π and 2π.

Cosine function period
The graph of the sine function has a period of 2π. This means that, after or before the range from 0 to 2π, the graph is periodic, that is, it repeats itself.
Parity
The sine function is considered a occupation impair, as there is symmetry in the graph in relation to the bisector of the odd quadrants. When a function is considered odd, we have to f (x) = -f (x), that is, sin (-x) = -sin (x).
Notable arcs of the sine function
Let's look at the sine value for the main angles:

Tangent function
We know that the tangent is the reason between sine and cosine. Unlike the two previous trigonometric functions, the tangent function has neither a maximum nor a minimum value. Also, there are restrictions for the domain, but the law of formation of the tangent function is f(x) = tan (x).
Domain
The tangent function has restrictions for its domain, as it is formed by the ratio between the sine and the cosine, there are no values for tangent when cos (x) = 0. Weighing in the trigonometric cycle from 0º to 360º, the tangent function is not defined for the 90º and 270º angles, as these are the values where the cosine is equal to 0. When there are angles greater than one full revolution, all those where the cosine value is 0 are not part of the domain of the cosine function.
Image
Unlike the sine function and the cosine function, the image of the tangent function is the set of real numbers, that is, it is not limited and has no maximum or minimum value. Im = R
Tangent function graph
The tangent function is also periodic like the sine and cosine functions, that is, it is always repeated. When we compare:

Signal
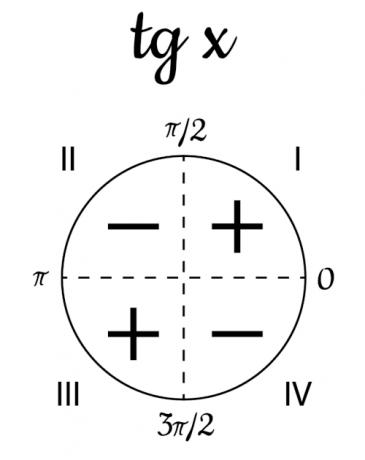
the tangent function has a positive value for the odd quadrants, that is, I and III quadrants. For angles between 0º and 90º and angles between 180º and 270º, the function has positive values. In radians, the value of x must be between 0 and π/2 or π and 3π/2.
Time course
The period of the tangent function is also different from the sine and cosine functions. O period of the tangent function is π.
Parity
the tangent function é an odd function, because tan(-x) = -tan (x), so there is symmetry in the graph with respect to the origin of the Cartesian plane.
Remarkable arcs of the tangent function
Let's look at the tangent value for the main angles:

See too: How to find sine and cosine of supplementary angles?
solved exercises
Question 1 - (Enem 2017) Rays of sunlight are reaching the surface of a lake, forming an angle x with its surface, as shown in the figure.
Under certain conditions, it can be assumed that the luminous intensity of these rays, on the lake surface, be given approximately by I(x) = k · sin(x), k being a constant, and assuming that X is between 0° and 90º.
When x = 30º, the luminous intensity is reduced to what percentage of its maximum value?
A) 33%
B) 50%
C) 57%
D) 70%
E) 86%
Resolution
Alternative B
In the range from 0º to 90º, the sine function has its highest value when x = 90º, so we have to:
i = k · sin (90º)
i = k · 1
i = k
Now, when x = 30º, we have to:
i = k · without (30th)
i = k · 1/2
i = k/2
Note that intensity i has been reduced by half, ie 50%.
Question 2 - (Enem 2015) According to the Brazilian Institute of Geography and Statistics (IBGE), seasonal products are those that present well-defined cycles of production, consumption and price. Briefly, there are times of the year when its availability in retail markets is scarce, with high prices, sometimes it is abundant, with lower prices, which occurs in the month of maximum production of the harvest. From a historical series, it was observed that the price P, in reais, of the kilogram of a certain seasonal product can be described by the function:

Where x represents the month of the year, where x = 1 associated with the month of January, x = 2, with the month of February, and so on, until x = 12, associated with the month of December.
In the harvest, the month of maximum production of this product is
A) January.
B) April.
C) June.
D) July.
E) October.
Resolution
Alternative D
The harvest admits maximum production when the price is the lowest, we know that the cosine function assumes its minimum value when cos(x) = -1.
The angle that has a cos value of -1 is the angle π. So the angle argument has to be equal to π, so we have to:
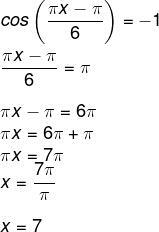
Month 7 is the month of July.
By Raul Rodrigues de Oliveira
Maths teacher