What is fraction?

Fraction is the mathematical representation of the parts of a given quantity that have been divided into equal pieces or fragments.

Fractions are useful in many situations, mainly to represent something that we cannot present with natural numbers.

Writing of a fraction and meaning of each term

Let's use the following situation as an example:

Maria bought a pizza and divided it into 4 equal slices. As she wasn't very hungry, she only ate one slice. What fraction of pizza did Maria know?

We see in the text above that of the 4 slices of pizza that Maria had, she ate only one, that is, 1 of 4. This can be written as a fraction:

table row with spaced cell 1 space in lower frame closes frame end of cell arrow to left numerator row with 4 left arrow denominator row with blank blank blank end of table

The terms of a fraction are:

Numerator: comes from latin numeratus and it means “to count”.

Denominator: its origin is from latin denominatus and it means “name”.

In our example, the number 1 represents the numerator of the fraction and indicates how many parts were taken. The number 4, on the other hand, represents the denominator of the fraction and indicates how many parts the whole was divided into.

instagram story viewer

Because you have divided the pizza into 4 equal parts, then a whole pizza corresponds to the fraction 4 over 4 .

4 over 4 space equals 1 space , that is, an integer.

Rules for reading fractions

The denominator of a fraction must be non-zero and it is what names the fraction. So we repeat the numerator and change the way we pronounce the denominator.

When the denominator is between the numbers 2 and 9, we read as follows: 2 (middle), 3 (third), 4 (fourth), 5 (fifth), 6 (sixth), 7 (seventh), 8 (eighth) and 9 (ninth).

As for decimal fractions, that is, with denominator 10, 100, 1000…, we use the nomenclature: 10 (tenths), 100 (hundredths), 1000 (thousandths), and so on.

For the other numbers, that is, those after 9 and not decimals, we use the word avos after the denominator.

Below are examples of fractions, their terms and how they should be read.

Numerator	Denominator	Reading
a	two	a way
two	three	two thirds
three	four	three bedrooms
seven	eight	seven eighths
eight	eleven	eight eleven
seven	twenty-one	seven twenty one
nine	ten	nine tenths
nine	hundred	nine hundredths

See too: Types of fractions and fractional operations

Types of fractions

mixed fraction

It is formed by two terms: one represents an integer quantity and the other corresponds to the fractional part.

Example:

$Mixed fraction example$

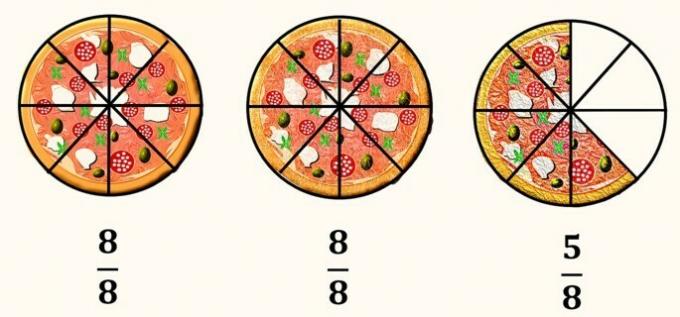
Note that each pizza has been divided into 8 equal parts and each one represents an integer, that is, 8 over 8 .

The amount of pizza we see in the image corresponds to two whole pizzas, with 16 slices, plus 5/8, that is, 5 slices of a pizza divided into 8 parts.

So we have:

$numerator 21 space over denominator 8 end of fraction equals numerator 8 space over denominator 8 end of fraction space plus space numerator 8 space over denominator 8 end of fraction space plus space 5 over 8 space equals space 1 space plus space 1 space space plus 5 over 8 space equal to space 2 space plus space 5 over 8 space or comma space simply comma space 2 space 5 about 8.$

The mixed fraction is read as follows: two integers and five eighths.

$table row with blank cell with space space space 2 end of cell cell with space space 5 space space in lower frame close frame end of cell blank blank blank row with cell with part full space end of cell down arrow with left corner 8 blank blank blank row with blank blank down arrow blank blank blank line with blank blank fractional part blank blank line with blank blank blank blank blank blank end of table$

know more about addition and subtraction of fractions.

equivalent fraction

equivalent fractions they are apparently different fractions, but they represent the same part of the whole.

Example: see below the amount of pizza consumed.

$Example of equivalent fractions$

By dividing a pizza into 8, 4 and 2 equal parts, respectively, and eating half of it, we will be consuming the same amount of pizza.

Therefore, the fractions 4 over 8 , 2 over 4 and 1 half are equivalent fractions and represent the same amount.

Note that the simplified form of fractions 4 over 8 and 2 over 4 é 1 half .
$4 to the power of divided by 4 end of exponential over 8 to power of divided by 4 end of exponential equal to numerator space 1 space over denominator 2 end of fraction 2 to the power of divided by 2 end of exponential over 4 to power of divided by 2 end of exponential equal to space numerator 1 space over denominator 2 end of fraction$

By simplifying the fractions, dividing the numerator and denominator by the same number, we arrive at a irreducible fraction, which corresponds to a fraction that can no longer be simplified.

In addition to the examples seen, fractions are also classified as:

Own fraction: fraction less than an integer, as the numerator is less than the denominator. Example:
improper fraction: fraction greater than an integer, as the numerator is greater than the denominator. Example:
apparent fraction: can be written as an integer, as the denominator is a divisor of the numerator. Example:
generating fraction: dividing the numerator by the denominator results in a periodic decimal. Example:

know more aboutgenerating fraction.

Solved exercises on fractions

question 1

Look at the puzzle below and answer:

a) What fraction represents the unassembled part?

See Answer

Correct answer: 1/3 (Read a third).

To write the fraction it is first necessary to find the denominator, which corresponds to the total number of pieces needed to fill the puzzle.

Counting the pieces, including the ones that are missing, we arrive at the result of 9 pieces. The numerator will then be the missing pieces, ie 3.

The fraction found is 3 over 9 . However, this result can still be simplified, as 3 and 9 have a common divisor, which is the number 3.

3 to the power of divided by 3 end of exponential over 9 to power of divided by 3 end of exponential equal to 1 third

Simplifying the terms of the fraction, we arrive at the fraction that represents the unassembled part, which is 1 third .

Learn more aboutfraction simplification.

b) What fraction represents the assembled part?

See Answer

Correct answer: 2/3 (Read two-thirds).

As we saw in the previous alternative, the denominator of the fraction is 9, since it corresponds to the total number of pieces of the puzzle.

The fraction numerator can be calculated by subtracting the total number of pieces from the number of missing pieces.

9 - 3 = 6

Thus, putting the values in the form of a fraction, we have 6 over 9 . Note that these numbers can be simplified if we divide both by 3.

After simplifying the terms of the fraction, we find that the fraction representing the assembled part is 2 on 3 .

For more questions, seeexercises on fractions.

c) What fraction represents the complete puzzle?

See Answer

Correct answer: 9/9

This fraction can be found by adding the fraction corresponding to the missing part and the fraction corresponding to the filled part.

3 over 9 space plus 6 over 9 space equals 9 over 9

The three missing pieces plus the six that are already assembled give us the number 9 in the numerator. The denominator corresponds to the total number of pieces, which is 9.

Note that all puzzle pieces are the same size. This is also the case with a fraction, as it also represents division into equal parts.

You may also be interested inmultiplication and division of fractions.

question 2

Write in the form of mixed and improper fraction the fraction that corresponds to the pie slices they contain in the image below.

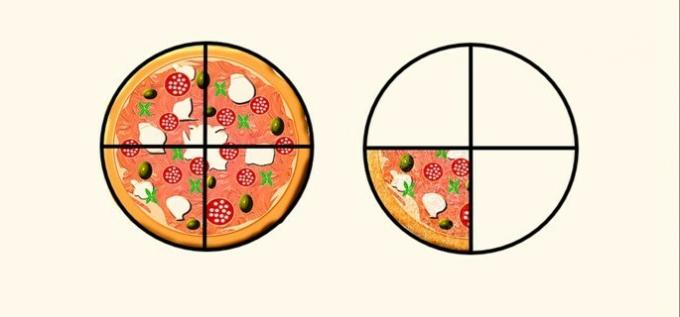
$pizza fraction study$

See Answer

Correct answer: mixed fraction 1 1/4 and improper fraction 5/4.

The first step is to assign each slice of pizza the corresponding fraction.

See that each pizza has been divided into 4 equal parts. Therefore, each slice represents 1 bedroom .

Adding the pie slices that are present in the image, we find the improper fraction, that is, the numerator is greater than the denominator.

1 room space more space 1 room space more space 1 room space more space 1 room space more space 1 room space equal to space 5 on 4

The mixed fraction consists of separating the whole part from the fractional part. Since we have a whole pizza and only 1 slice on the second pizza, the corresponding fraction is: