Electric Current Exercises

Electric current represents the amount of charge that passes through a conductor per unit of time. The unit of electrical current in the international system is the ampere (A).

In calculations of electrical circuits we often have to calculate the current passing through their terminals. Being a very charged content in college entrance exams.

So, don't miss the opportunity to check your knowledge by trying the exercises below and following the proposed resolutions.

Resolved and Commented Issues

1) UERJ - 2019

Identical ohmic resistors were combined in four different circuits and subjected to the same voltage U_{A, B}. Look at the schematics:

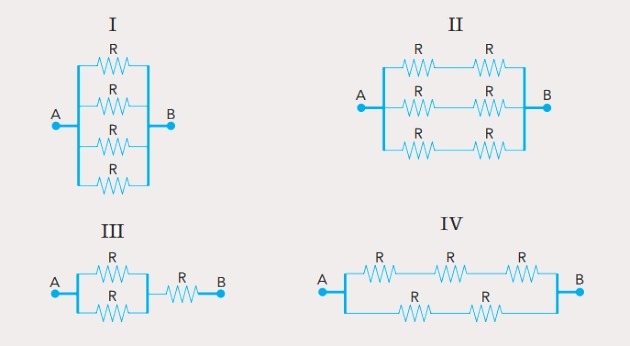
Under these conditions, the electrical current of lesser intensity is established in the following circuit:

there
b) II
c) III
d) IV

See Answer

Since the resistors are ohmic, we can apply Ohm's law in the 4 proposed circuits, ie:

U_{A, B} = R_eq.i

Analyzing this relationship, we conclude that if the voltage at terminals AB is the same for all circuits, then the one with the highest equivalent resistance will have less current.

Therefore, we need to calculate the equivalent resistance in each circuit.

I) We have four resistors associated in parallel. In this way, the equivalent resistance will be found by doing:

II) In this circuit, the resistors are associated in series and parallel (mixed association). We have three branches, with two resistors associated in series in each branch.

We start by finding the equivalent resistance of the series. So we have:

In this way, the circuit can be replaced by a parallel circuit, with a 2R resistor in each of the 3 branches.

We can now calculate the equivalent resistance of the parallel association which will be the equivalent resistance of the circuit:

III) This is also a mixed circuit, with two resistors associated in parallel and in series with a third resistor.

Finding the equivalent resistance of the parallel, we have:

The equivalent resistance of the circuit is found by adding the equivalent resistance of the parallel with the resistance R, so we have:

IV) We now have three series resistors associated in parallel with two other series resistors. Let's first find the equivalent resistance of each series:

Now, we will find the equivalent resistance of the circuit by calculating the equivalent resistance of the parallel:

Now that we've found the equivalent resistances for each circuit, we have to identify which is the largest. Being:

We conclude that in circuit III, which has the highest resistance, we will have the lowest current intensity.

Alternative: c) III

2) Enem - 2018

Some fish, such as the poraquê, the electric eel from the Amazon, can produce an electric current when they are in danger. A 1-meter long, endangered pork produces a current of around 2 amps and a voltage of 600 volts.

The table shows the approximate power of electrical equipment.

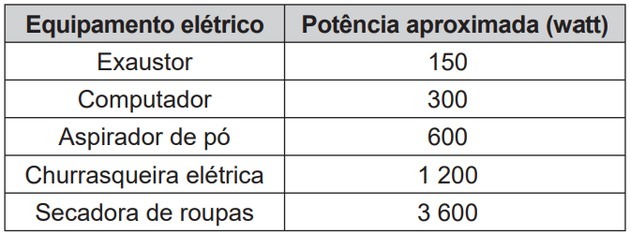
The electrical equipment that has power similar to that produced by this endangered fish is the

a) The exhaust fan.
b) computer.
c) vacuum cleaner.
d) electric barbecue.
e) clothes dryer.

See Answer

First we need to find out what the value of the potency produced by the fish is, for that we will use the potency formula and substitute the presented values:

Comparing with the data in the table, we identified that this power is equivalent to an electric barbecue.

Alternative: d) electric barbecue.

3) PUC/RJ - 2018

In an electrical circuit, two identical resistors, of resistance R, are installed in parallel and connected, in series, to a battery and a third resistor, identical to the previous ones. In this configuration, the current flowing through the circuit is I₀. When replacing this third resistor in series with another resistor of 2R, the new current in the circuit will be

there₀
b) 3I₀/5
c) 3I₀/4
d) I₀/2
Hey₀/4

See Answer

In the first situation, the equivalent resistance will be given by:

In the second situation, the resistor resistance in series changes to 2R, so the equivalent resistance in this new situation will be equal to:

As there was no change in the value of the battery that feeds the circuit, then the voltage is the same in both situations. Considering Ohm's law, we have the following equalities:

Alternative: b) 3I₀/5

4) Enem - 2017

In some homes, electrified fences are used to keep out potential intruders. An electrified fence works with an electrical potential difference of approximately 10,000 V. In order not to be lethal, the current that can be transmitted through a person must not be greater than 0.01 A. The body electrical resistance between a person's hands and feet is in the order of 1 000 Ω.

In order for the current not to be lethal to a person touching the electrified fence, the voltage generator must have an internal resistance that, in relation to that of the human body, is:

a) practically null.
b) approximately equal.
c) thousands of times larger.
d) of the order of 10 times larger.
e) on the order of 10 times smaller.

See Answer

For this question we will use the equation of a generator, as we want to compare the internal resistance of the generator with the resistance of the human body. This equation is given by:

Being:

U: the circuit potential difference (V)
ε: electromotive force (V)
r: internal generator resistance (Ω)
i: current (A)

The value of U can be found using Ohm's law, ie U = R.i. Note that this resistance is the circuit resistance, which in this case is equal to the body resistance.

Substituting the problem values ​​in the generator equation, we have:

Now we need to find out how many times the generator's internal resistance must be greater than the body's resistance. For this, let's divide one by the other, that is:

Therefore, the internal resistance of the generator should be around 1000 times greater than the resistance of the person's body.

Alternative: c) thousands of times larger.

5) Enem - 2016

Three identical lamps were connected in the schematic circuit. The battery has negligible internal resistance, and the wires have zero resistance. A technician performed a circuit analysis to predict the electrical current at points: A, B, C, D, and E; and labeled these currents I_THE, I_B, I_Ç, I_D Hey_AND, respectively.

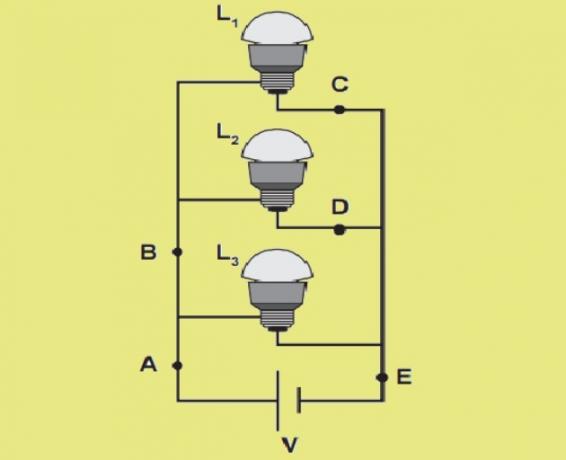
The technician concluded that the chains that have the same value are

there_THE = I_AND Hey_Ç = I_D.
b) I_THE = I_B = I_AND Hey_Ç = I_D.
c) I_THE = I_B, only.
d) I_THE = I_B = I_AND, only.
Hey_Ç = I_B, only.

See Answer

In the diagram below we represent the currents that flow through the various branches of the circuit.

Following the scheme, we observe that I_THE Hey_B are the same and that I_ç Hey_D are also the same.

Alternative: a) I_THE = I_AND Hey_Ç = I_D

6) Enem PPL - 2016

Electric shock is a sensation caused by the passage of electric current through the body. The consequences of a shock range from a simple scare to death. The circulation of electrical charges depends on the material's resistance. For the human body, this resistance ranges from 1 000 Ω when the skin is wet, to 100 000 Ω when the skin is dry. A barefoot person, washing his house with water, got his feet wet and accidentally stepped on a bare wire, suffering an electrical discharge at a voltage of 120 V.

What is the maximum intensity of electrical current that passed through the person's body?

a) 1.2 mA
b) 120 mA
c) 8.3 A
d) 833 A
e) 120 kA

See Answer

We want to discover the maximum current that runs through the person's body. Note that we have two resistance values, one for the dry body and one for the wet body.

The maximum current, since the person is in a wet body, will be found considering the minimum value given for the resistance, ie 1000 Ω.

Considering this value, let's apply Ohm's law:

Alternative: b) 120 mA

7) Fuvest - 2010

Electrical measurements indicate that the earth's surface has a total negative electrical charge of approximately 600,000 coulombs. In storms, positively charged rays, although rare, can reach the earth's surface. The electrical current of these rays can reach values ​​of up to 300,000 A. What fraction of the Earth's total electrical charge could be offset by a radius of 300,000 A and a duration of 0.5 s?

a) 1/2
b) 1/3
c) 1/4
d) 1/10
e) 1/20

See Answer

The current value is found by applying the following formula:

Being:

i: current (A)
Q: electric charge (C)
Δt: time interval(s)

Replacing the indicated values, we find:

To know the fraction of the Earth's total electrical charge that could be compensated by the radius, let's do the following reason:

Alternative: c) 1/4

To learn more, see also:

• Resistor Association - Exercises
• Association of Trainers
• Physics Formulas