Newton's Laws: Commented and Solved Exercises

At Newton's laws comprise three laws of Classical Mechanics: the law of inertia, the fundamental law of dynamics, and the law of action and reaction.

Test your knowledge with the 8 questions below and don't miss the opportunity to clarify your doubts by following the resolutions after the feedback.

question 1

Relate Newton's three laws to their respective statements.

1. Newton's 1st Law
2. Newton's 2nd Law
3. Newton's 3rd Law

Determines that the net force is equal to the product of the mass and the acceleration of the body.

It states that to every action there is a reaction of the same intensity, same direction and opposite direction.

Indicates that a body tends to remain in its state of rest or in uniform rectilinear motion, unless a resultant force acts on it.

See Answer

Correct answer: (2); (3) and (1).

law of inertia (1st Law of Newton): indicates that a body tends to remain in its state of rest or in uniform rectilinear motion, unless a resultant force starts to act on it.

Fundamental law of dynamics

(2nd Law of Newton): determines that the resulting force is equal to the product of mass and acceleration of the body.

law of action and reaction (3rd Law of Newton): states that to every action there is a reaction of the same intensity, same direction and opposite direction.

question 2

(UFRGS - 2017) A force of 20 N is applied to a body of mass m. The body moves in a straight line with a speed that increases by 10 m/s every 2 s. What is the value, in kg, of the mass m?

a) 5.
b) 4.
c) 3.
d) 2.
e) 1.

See Answer

Correct alternative: b) 4.

To find the mass value, let's apply Newton's second law. For that, we first need to calculate the acceleration value.

As the acceleration is equal to the velocity variation value divided by the time interval, we have:

Replacing the found values:

Therefore, the body mass is 4 kg.

question 3

(UERJ - 2013) A wooden block is balanced on an inclined plane of 45º in relation to the ground. The intensity of the force that the block exerts perpendicularly to the inclined plane is equal to 2.0 N.

Between the block and the inclined plane, the intensity of the friction force, in newtons, is equal to:

a) 0.7
b) 1.0
c) 1.4
d) 2.0

See Answer

Correct alternative: d) 2.0.

In the diagram below we represent the situation proposed in the problem and the forces that act in the block:

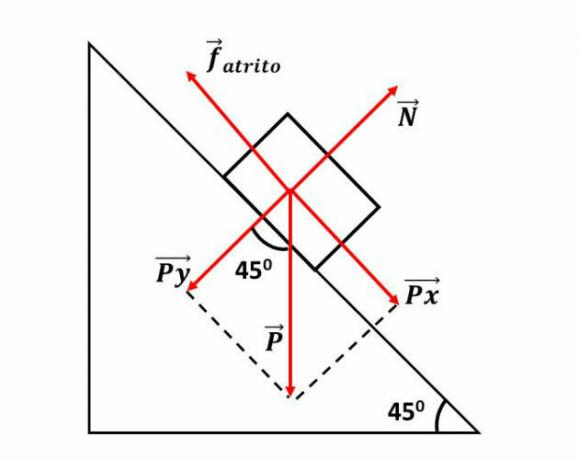
Since the block is in equilibrium on the inclined plane, the net force on both the x-axis and the y-axis is equal to zero.

Thus, we have the following equalities:

f_friction = P. sen 45th
N = P. cos 45th

If N is equal to 2 N and sin 45° is equal to cos 45°, then:

f_friction = N = 2 newtons

Therefore, between the block and the inclined plane, the friction force intensity is equal to 2.0 N.

See too:

inclined plane

Frictional force

question 4

(UFRGS - 2018) The tug of war is a sporting activity in which two teams, A and B, pull a rope by the opposite ends, as shown in the figure below.

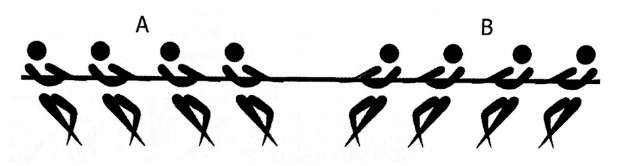
Assume that the rope is pulled by team A with a horizontal force of modulo 780 N and by team B with a horizontal force of modulo 720 N. At a given moment, the rope breaks. Check the alternative that correctly fills in the blanks in the statement below, in the order in which they appear.

The net force on the string, at the instant immediately before the break, has a modulus of 60 N and points to ________. The modules of the accelerations of teams A and B, at the instant immediately after the rope is broken, are, respectively, ________, assuming that each team has a mass of 300 kg.

a) left - 2.5 m/s² and 2.5 m/s²
b) left - 2.6 m/s² and 2.4 m/s²
c) left - 2.4 m/s² and 2.6 m/s²
d) right - 2.6 m/s² and 2.4 m/s²
e) right - 2.4 m/s² and 2.6 m/s²

See Answer

Correct alternative: b) left - 2.6 m/s² and 2.4 m/s².

The resulting force points to the direction of greatest force, which in this case is the force exerted by team A. Therefore, its direction is to the left.

In the instant immediately after the string snaps, we can calculate the amount of acceleration acquired by each team through Newton's second law. So we have:

Therefore, the text with the gaps filled in correctly is:

The resulting force on the rope, at the instant immediately before the break, has a modulus of 60 N and points to the left. The modules of the accelerations of teams A and B, at the instant immediately after the break of the rope, are, respectively, 2.6 m/s² and 2.4 m/s², assuming that each team has a mass of 300 kg.

See too: Newton's Laws

question 5

(Enem - 2017) In a frontal collision between two cars, the force that the seat belt exerts on the driver's chest and abdomen can cause serious damage to the internal organs. With the safety of its product in mind, a car manufacturer conducted tests on five different belt models. The tests simulated a 0.30-second collision, and the dolls representing the occupants were equipped with accelerometers. This equipment records the modulus of the doll's deceleration as a function of time. Parameters such as doll mass, belt dimensions and speed immediately before and after impact were the same for all tests. The final result obtained is in the graph of acceleration by time.

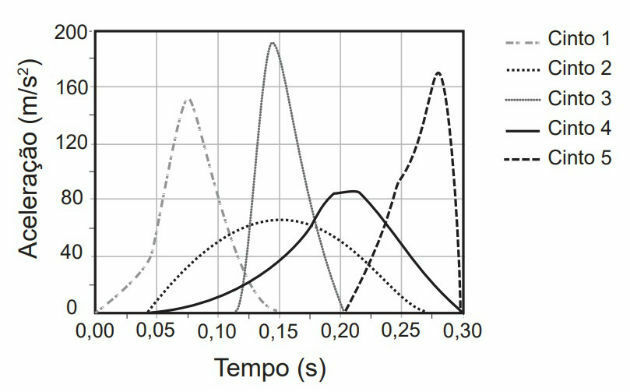
Which belt model offers the lowest risk of internal injury to the driver?

to 1
b) 2
c) 3
d) 4
e) 5

See Answer

Correct alternative: b) 2.

The problem tells us that the force exerted by the seat belt can cause serious injuries in head-on collisions.

Therefore, we need to identify, among the models presented and under the same conditions, the one that will exert a less intense force on the passenger.

By Newton's second law, we have that the resulting force is equal to the product of mass and acceleration:

F_R = m. The

As the experiment was carried out using puppets of the same mass, then the lowest resultant force on the passenger will occur when the maximum acceleration is also smaller.

Observing the graph, we identify that this situation will occur in belt 2.

See too: Newton's Second Law

question 6

(PUC/SP - 2018) A cubic, massive and homogeneous object, with a mass equal to 1500 g, is at rest on a flat and horizontal surface. The coefficient of static friction between the object and the surface is equal to 0.40. A force F, horizontal to the surface, is applied over the center of mass of that object.

Which graph best represents the intensity of the static friction force F_friction as a function of the intensity F of the applied force? Consider the forces involved in SI units.

See Answer

Correct alternative: c.

In the situation proposed by the problem, the body is at rest, so its acceleration is equal to 0. Considering Newton's 2nd Law (F_R = m. a), then the net force will also equal zero.

As described in the problem, there is force F and friction force acting on the body. In addition, we also have the action of weight force and normal force.

In the figure below, we present the diagram of these forces:

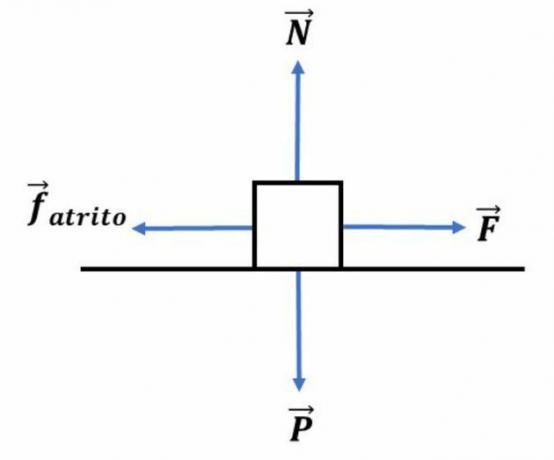
On the horizontal axis, while the body remains at rest, we have the following situation:

F_R = F - F_friction = 0 ⇒ F = F_friction

This condition will be true until the value of force F reaches the intensity of the maximum friction force.

The maximum friction force is found through the formula:

From the figure presented above, we notice that the value of the normal force is equal to the intensity of the weight force, since the body is at rest on the vertical axis. Then:

N = P = m. g

Before replacing the values, we must transform the mass value to the international system, ie 1500 g = 1.5 kg.

N = 1.5. 10 = 15 N

Thus, the value of F_frictionmax will be found by doing:

F_frictionmax= 0,4. 15 = 6 N

Therefore, the F_friction on the body it will be equal to force F until it reaches the value of 6N, when the body will be on the verge of movement.

question 7

(Enem - 2016) An invention that meant a great technological advance in Antiquity, the composite pulley or the association of pulleys, is attributed to Archimedes (287 a. Ç. to 212 a. Ç.). The apparatus consists of associating a series of mobile pulleys with a fixed pulley. The figure exemplifies a possible arrangement for this apparatus. It is reported that Archimedes would have demonstrated to King Hieram another arrangement of this apparatus, moving alone, over the sand on the beach, a ship full of passengers and cargo, something that would be impossible without the participation of many men. Suppose the ship's mass was 3000 kg, the coefficient of static friction between the ship and the sand was 0.8, and that Archimedes pulled the ship with a force , parallel to the direction of movement and with a modulus equal to 400 N. Consider the ideal wires and pulleys, gravity acceleration equal to 10 m/s² and that the beach surface is perfectly horizontal.

The minimum number of mobile pulleys used, in this situation, by Archimedes was

a) 3.
b) 6.
c) 7.
d) 8.
e) 10.

See Answer

Correct alternative: b) 6.

The forces acting on the boat are represented in the diagram below:

From the diagram, we notice that the boat, to come out of rest, requires the tractive force T to be greater than the maximum static friction force. To calculate the value of this force, we will use the formula:

In this situation, the weight modulus is equal to the normal force modulus, we have:

Replacing the values ​​informed, we have:

F_{friction max} = 0,8. 3000. 10 = 24 000 N

We know that the force F exerted by Archimedes was equal to 400 N, so this force must be multiplied by a certain factor so that its result is greater than 2400 N.

Each mobile pulley used doubles the force value, that is, making a force equal to F, the traction force (the force that will pull the boat) will be equal to 2F.

Using the problem data, we have the following situation:

• 1 pulley → 400. 2 = 400. 2¹ = 800 N
• 2 pulleys → 400. 2. 2 = 400. 2 ² = 1600 N
• 3 pulleys → 400. 2. 2. 2 = 400. 2³ = 3200 N
• n pulleys → 400. 2^no > 24,000 N (to come out of rest)

Thus, we need to know the value of n, so:

We know that 2⁵ = 32 and that 2⁶ = 64, as we want to find the minimum number of moving pulleys, then using 6 pulleys it will be possible to move the boat.

Therefore, the minimum number of mobile pulleys used, in this situation, by Archimedes was 6.

question 8

(UERJ - 2018) In one experiment, blocks I and II, with masses equal to 10 kg and 6 kg, respectively, are interconnected by an ideal wire. At first, a force of intensity F equal to 64 N is applied to block I, generating a tension T on the wire._THE. Then, a force of the same intensity F is applied to block II, producing traction T_B. Look at the schematics:

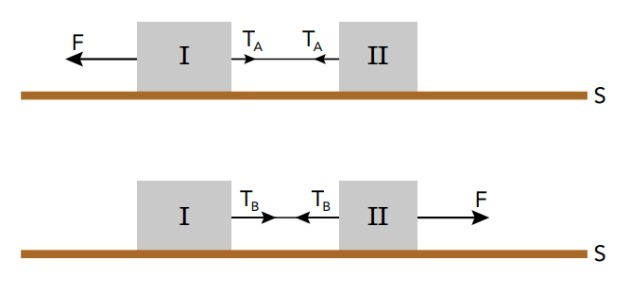
Disregarding the friction between the blocks and the surface S, the ratio between the tractions stands for:

See Answer

Correct alternative: .

Applying Newton's second law and the law of action and reaction (Newton's third law), we can write the systems for each situation:

1st situation

2nd situation

Note that in both situations the acceleration value will be the same, as the force F is equal and the masses also remain the same.

Replacing the values ​​and calculating the acceleration, we have:

Knowing the acceleration value, we can calculate the values ​​of the tractions:

T_THE = m_II. The
T_THE = 6. 4 = 24 N

T_B = m_I . The
T_B = 10. 4 = 40 N

Calculating the ratio between the pulls, we find:

Therefore, the ratio between the pulls corresponds to .

To learn more, see also:

• Newton's Third Law
• strength weight
• Normal force