At multiplication properties can be found in the sets numbers that we study throughout primary school.
In multiplication we have: commutative property, associative property, distributive property, neutral element and inverse element.
Concept and properties of multiplication
We know that the multiplication is nothing but the realization of successive sums, for example, when we multiply 3 · 5 it's the same as adding 3 by itself five times or 5 by itself three times, see:
3 + 3 + 3 + 3 + 3 = 15
5 + 5 + 5 = 15
Thus, 3 · 5 = 15, but note that doing this process is not always the best way, try calculating 9 · 8 using this method. Of course it's not an impossible task, just a very complicated one. We will see below some properties that facilitate this process, these properties are all from the properties of the addition.
Read too: Multiplication of algebraic fractions: how to do it?
Commutative property of multiplication
Multiplication satisfies commutativity, that is, given two real numbers, a and b, we can
multiply them in whatever order we want, the result will always be the same. We can write such a property as follows:a · b = b · a
Example
Note the 5 · 4 multiplication and the 4 · 5 multiplication.
5 · 4 = 20
4 · 5 = 20
This property is inherited from addition, since the multiplication operation is nothing more than successive additions of the same number.
Caution: commutativity is valid for real numbers/complexes, but, in the set of matrices, this operation is not satisfied, that is, given two matrices: A · B ≠ B · A.
Read too: Matrix multiplication: how to calculate?
Associative property of multiplication
The associative property of multiplication tells us that in the multiplication of three numbers we can choose the order of the products. Generally speaking, we can represent this property like this:
(a · b) · c = a · (b · c)
Example
Watch:
(3 · 5) · 2 = 15 · 2 = 30, on the other hand 3 · (5 · 2) = 3 · 10 = 30.
Note that we can multiply any of the factors first, the final result still holds.
Distributive property of multiplication
In multiplication we can distribute the product, this occurs when we go multiply a number by a sum.
a · (b + c) = a · b + a · c
Consider the following multiplication: 3 · (5 + 4).
On the one hand, we have to:
3 · (5 + 4) =
3 · 9 =
27 =
On the other hand, we can perform the distributivity, which consists of multiplying the number outside the parenthesis by each term of the sum, so we have to:
3 · (5 + 4) =
3 · 5 + 3 · 4 =
15 + 12 =
27 =
See that:
3 · (5 + 4) = 3 · 5 + 3 · 4
neutral element
The neutral element is the one that, when operated with any other number, keeps as a result the number with which it was operated. In the case of multiplication, the neutral element is number 1, i.e:
a · 1 = a
Examples
The) 2 · 1 = 2
B) 309 · 1 = 309
ç) –10000 · 1 = – 10000
inverse element
The inverse element in multiplication is the one that when multiplied by a number results in 1. The inverse element of a number The It is given by:

Thus, the inverse of any number is always the fraction one over the number.
Examples
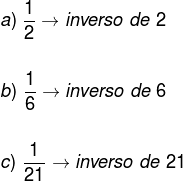

solved exercises
question 1 – Determine the value of x in the expression x (2 – x) = 0
Solution
To determine the value of x in the expression, we have to use the distributive property of multiplication, like this:
x (2 - x) = 0
2x - x2 = 0
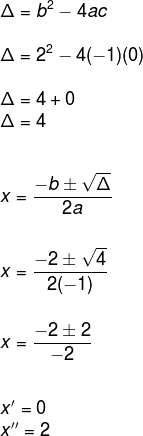
question 2 – It is known that the inverse of a number is equal to the eighth part of that number plus a quarter. Determine that number.
Solution
Since we don't know the number, let's name it y. By the statement, the inverse is equal to the eighth part of this number y added by a quarter, so we have the following equality:
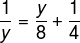
Resolving the previous equality, we have:
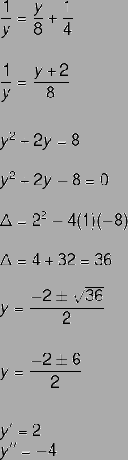
by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/propriedades-multiplicacao-que-facilitam-calculo-mental.htm

