In the study of the modular number, the modulus consists of the absolute value of a number (x) and is indicated with |x|, the non-negative real number that satisfies:

However, we will study inequalities involving modular numbers, thus consisting of modular inequalities.
Using the previous property, let's see an inequality:
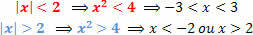
These situations are repeated for the other numbers, so let's see, in general, such a situation for a k (positive real) value.

Knowing this property, we are able to solve modular inequalities.
Example 1) Solve the inequality |x – 3|< 6.
For the property, we have to:
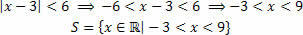
Example 2) Solve the inequality: |3x – 3| ≥ 2x + 2.
We need to determine the values of the module, with that, we have:
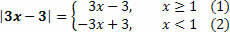
Therefore, we will have two possibilities for inequality. Therefore, we must analyze two inequalities.
1st possibility:

By intersecting inequalities (3) and (4), we obtain the following solution set:

2nd possibility:

Making the intersection of inequalities (5) and (6), we obtain the following solution set:

Therefore, the solution is given by the union of the two obtained solutions:
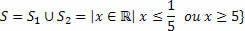
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Source: Brazil School - https://brasilescola.uol.com.br/matematica/inequacao-modular.htm
