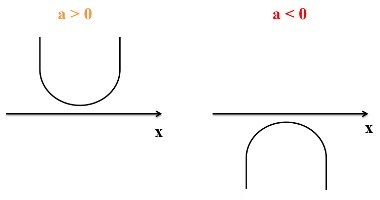
Functions that are expressed by the formation law y = ax + b or f (x) = ax + b, where a and b belong to the set of real numbers, with a ≠ 0, are considered 1st degree functions. This type of function can be classified according to the value of the coefficient a, if a > 0, the function is increasing, if a < 0, the function becomes decreasing.
Let's analyze the following functions f (x) = 3x and f (x) = –3x, with domain over the set of real numbers as the values of x increase.
Example 1
f (x) = 3x


Note that as the values of x increase, the values of y or f(x) also increase, in which case we say that the function is increasing and the rate of change of the function is equal to 3.
Example 2
f (x) = –3x 
Do not stop now... There's more after the advertising ;)

In this situation, as the values of x increase, the values of y or f(x) decrease, so the function becomes decreasing and the rate of change has a value of –3.
Another important fact to designate a function is its graph, note that when the function is increasing the angle formed between the line of the function and the x axis (horizontal) is acute (< 90º) and in the decreasing function the angle formed is obtuse (> 90º).
Then, the function is increasing over the set of real numbers (R), when the values of x1 and x2, where x1 < x2 result in f (x1) < f (x2). In the case of the decreasing function on the set of reals, we will have x1 < x2 resulting in f (x1) > f (x2).
by Mark Noah
Graduated in Mathematics
Brazil School Team
1st degree function - Roles- Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Ascending function and descending function"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcao-crescente-funcao-decrescente.htm. Accessed on June 28, 2021.