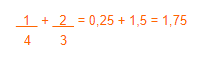We know as real numbers all rational numbers and irrational. By studying the numerical sets, it is important to understand that they follow the needs and history of humanity, the numerical sets are:
- set of natural numbers
- whole number set
- set of rational numbers
- set of irrational numbers
- set of real numbers
You real numbers have properties such as: associative, commutative, existence of the neutral element for addition and multiplication, existence of an inverse element in multiplication, and distributive. the real numbers can be represented on the real line — how to represent them in an orderly fashion.
Read too: What are prime numbers?
What are the real numbers?

We know as real numbers the set formed by union of rational and irrational numbers. It is quite common to work with them, but the set of real numbers was not the first to appear in history.
natural numbers
O first numerical set it was formed by the natural numbers. They were created from the basic need of human beings to count and to count objects of their daily lives. You natural numbers they are:
N = {0, 1, 2, 3, 4, 5, 6...}
integers
With the evolution of society, the yearnings of the human being were changing and the need to work with negative numbers. Operations like 4 – 6, which, in the set of natural numbers, did not make sense, began to do so with the emergence of this new set. The set of whole numbers came up with the addition of negative numbers in the set of natural numbers, that is, it is formed by the natural numbers and the opposite of them.
Z = {... -3, -2, -1, 0, 1, 2, 3...}
rational numbers
It turns out that, even so, with the addition of the negative numbers, the set of whole numbers was not enough, since the ancient egypt, it is quite common to use numbers that are not integers. It was then that the need to formalize a new set was realized: the set formed by all numbers that can be represented by a fraction is known as rational numbers.
Unlike the set of whole numbers, in the rational it is not possible to write a list of terms with their predecessors and successors, because, given the rational numbers, there will always be another rational number between them. For example, between 1 and 2 there is 1.5; between 1 and 1.5 there is 1.25; and so on. Therefore, to represent the rational numbers, we use the following notation:
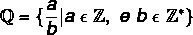
In this notation the rational number is the one that can be represented by the fraction The under B, on what The is an integer and B is a non-zero integer.
In the set of rational numbers, all integers were included that were already known, as they can all be represented as a fraction, in addition to the exact decimal numbers and the periodic tithes, positive and negative.
See too: What are ordinal numbers?
irrational numbers
Contrary to the definition of rational numbers, there are numbers that cannot be represented as a fraction. Some mathematicians have studied them in time, in an attempt to make this representation, but it is not possible. These numbers are the non-periodic tithes and the roots not exact, which end up generating non-periodic tithes as a result. The number π, for example, is an irrational number that is quite common in everyday life. The set of irrational numbers is not listable, as are rational numbers, and is represented by the letter I.
Examples:
- √2 → non-exact roots are irrational numbers;
- -√5 → roots not exact even if negative are irrational numbers;
- 3.123094921… → non-periodic decimals are irrational numbers.
real numbers
Since all natural and integer numbers are considered rational, so far, numbers can be classified into two large sets, the set of rational numbers and the set of numbers irrational. The set of real numbers is nothing more than the union of rational and irrational numbers.
R = {Q U I}
So far, all the numbers we know are called real numbers.
Operations with real numbers
The operations involving real numbers are those known for all previous sets of numbers. Are they:
- addition
- subtraction
- division
- multiplication
- potentiation
- radiciation
To perform any of these operations between real numbers, there is no difference from operations with previous numbers.
Also, considering such operations, it is important to highlight that there are properties in the set of real numbers.
Properties of real numbers
It is important to understand that the properties of real numbers are consequences of its definition and are useful for performing operations. Are they:
- existence of a neutral element for addition and multiplication
- commutative property
- associative property
- distributive property
- existence of an inverse
neutral element
Be The a real number.
There is a number that, added to The, results in itself The:
The + 0 = The
0 is the neutral element of the sum..
There is a number that, when multiplying by The, results in itself The.
The · 1 = The
1 is the neutral element of multiplication.
Commutative Property
Be The and B two real numbers.
In either addition or multiplication, the order of numbers will not change the result.
The + B = B + The
a · b = b · a
associative property
Be The, B and ç real numbers.
In both addition and multiplication, the two operated numbers are indifferent to any order.
(The + B) + ç = The + (B + ç)
(a · b) · ç = The· (b · c)
distributive property
Be The, B and ç real numbers.
The distributive property shows that the product of the sum is equal to the sum of the products.
ç (a + b) = ca+cb
Existence of an inverse
Be The a nonzero real number.
for every real number The different from zero, there is a number such that the product enters The and this number is equal to 1.

representation on the straight
We can represent the set of real numbers in a line, since there is a well-defined principle of order for him. This representation on the line is known as the real line or reit's numerical and it is quite common, even in the study of the Cartesian plane.

Also access: What is fraction?
solved exercises
Question 1 - Please judge the following statements:
I – Periodic decimals are real numbers.
II – Every real number is rational or irrational.
III – Not every whole number is natural.
By analyzing the statements, we can say that:
A) only I is false.
B) only II is false.
C) only III is false.
D) all are true.
E) all are false.
Resolution
Alternative D.
I – True, since the tithes are irrational numbers, consequently, they are real numbers.
II – True, since the set of real numbers is the union of real and irrational numbers.
III – True, as negative numbers, such as -2 and -5, are integers, but not natural.
Question 2 - Check out the following properties:
I - commutative property
II - distributive property
III - associative property
Analyze the following operations and mark them with the number of their respective properties:
1 - ( ) 3 (2 + 5) = 6 + 15
2 - ( ) 5 · 4 = 4 · 5
3 - ( ) (2 + 4) + 1 = 2 + (4 + 1)
4 - ( ) 1 + 5 = 5 + 1
Which of the alternatives corresponds to the correct order of properties:
A) II - I - III - I
B) I - III - III - II
C) III - II - III - III
D) II - I - III - II
E) II - III - II - I
Resolution
Alternative A.
1 - (II) In this case, the distributive property happened, since note that 3 was multiplied by each of the factors of the operation.
2 - (I) In this case, the order of the factors does not change the product, commutativity of multiplication.
3 - (III) We have the associative property, as the order in which these elements are added does not change the sum.
4 - (I) Here again we have commutativity, as the order of the parcels does not change the sum.