One fraction is a number that represents the division between two whole numbers. Fractions also represent one or many parts of an object that has been divided into equal parts. Are we now going to learn how to add or subtract them?
Addition and subtraction of fractions with equal denominators
When the fractions to be added have the same denominator, the result will be composed as follows:
Numerator: Sum of fraction numerators;
Denominator: Repeat the denominator, which is the same for all of them.
For example:
7 + 9 – 3 = 7 + 9 – 3 = 16 – 3 = 13
3 3 3 3 3 3
Note, in the example, that subtraction of fractions of equal denominators follows the same pattern as addition.
Addition or subtraction of fractions with different denominators
When the denominators are different, a matching procedure needs to be carried out. This procedure differentiates the fractions, but makes them equivalent, that is, with the same denominator. For example, look at the sum:
3 + 4 = 4 + 4 = 8 = 2
3 4 4 4 4
Note that both the 3/3 fraction and the 4/4 fraction are equal to 1 when dividing the numerator by the denominator. Any fraction having this result will be equivalent. So, we exchange the first for some fraction of denominator 4 that is equivalent to 1 and perform the sum of fractions with equal denominators.
However, it is not always easy to find these equivalent fractions. For this, there is a method that involves finding the Least common multiple between the denominators and that works for any addition or subtraction of fractions.
Let's solve an example? Look:
1 + 7
16 9
→ First step
Calculate the MMC between the denominators of the fractions to be added.
16, 9 |2
8, 9 |2
4, 9 |2
2, 9 |2
1, 9 |3
1, 3 |3
1, 1
MMC = 2·2·2·2·3·3 = 144
→ Second step
Use the found MMC as the denominator of the two new fractions.
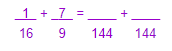
→ Third step
Divide the MMC by the denominator of the first fraction, multiply the result of this division by the numerator of that same fraction and put the final result as the numerator of the first fraction whose denominator is the MMC.
Division of MMC by 16:
144 | 16
-144 9
0
Now you multiply the result of this division by the numerator of the same fraction:
9·1 = 9
As the result of this multiplication is the numerator of the first fraction whose denominator is the MMC, then, updating the previous scheme, we will have:
1 + 7 = 9 +
16 9 144 144
→ Fourth step
Repeat the third and fourth steps above until the fractions to be added or subtracted have been exhausted. Watch:
Division of MMC by 9 (denominator of the second fraction):
144 | 9
-144 16
0
Now you multiply the result of this division by the numerator of the same fraction:
16·7 = 112
As the result of this multiplication is the numerator of the first fraction whose denominator is the MMC, then, updating the previous scheme, we will have:
1 + 7 = 9 + 112
16 9 144 144
→ Fifth step
Once the fourth step is finished, just add fractions with equal denominators. The only difference between adding and subtracting fractions is in this last step. If it's subtraction, instead of adding, subtract the numerators.
1 + 7 = 9 + 112 = 121
16 9 144 144 144
Addition and subtraction of decimal numbers
Another possibility of addition of fractions is to divide the numerator by the denominator of each of the fractions to be added and add the resulting decimals. For example:

Keep in mind that this rule also holds for subtraction. If you need to subtract two fractions, repeat this procedure and, instead of adding, subtract.
By Luiz Paulo Moreira
Graduated in Mathematics
Take the opportunity to check out our video lesson related to the subject: