The diamond is a quadrilateral that has the four sides congruent, that is, with the same measure. It is also composed of two diagonals: major diagonal (D) and minor diagonal (d). These two diagonals intersect at the midpoint of each other (exactly in the middle of them). Opposite angles of a diamond are also congruent.
Having understood the characteristics of a diamond, let's find out how its area is calculated.
The area of the diamond depends on the measurements of the two diagonals, so we say that the area is given as a function of the diagonals of the diamond. The formula for calculating the diamond area is:
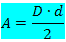
Where,
D → is the measure of the longest diagonal
d → is the measure of the minor diagonal.
Example 1. If a diamond has a larger diagonal measuring 10cm and a smaller diagonal measuring 7cm, what is its area value?
Solution: According to the exercise statement, we know that D = 10cm and d = 7cm. Since we know the values of the diagonals, let's apply the formula.
Therefore, the diamond has 35 cm2 of area.
Example 2. In a diamond, the measurement of the major diagonal is twice the measurement of the minor diagonal. Knowing that D = 50cm, what will be the measurement of the area of this diamond?
Solution: We know that the longest diagonal is twice the shortest diagonal. Since D = 50cm, we can say that d = 25cm. Once the diagonal measurements are known, just use the area formula.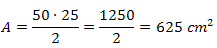
Therefore, the diamond is 625 cm2 of area.
Example 3. A diamond has an area equal to 60 m2. Knowing that the shortest diagonal measures 6m, find the length of the longest diagonal.
Solution: Since we know the measure of the area of the diamond and the shortest diagonal, we must use the area formula to find the measure of the longest diagonal.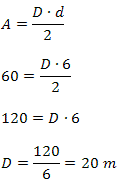
Therefore, the longest diagonal is 20m long.
By Marcelo Rigonatto
Mathematical
Kids School Team