Percentage it involves several situations that we frequently face in our daily lives, for example in economic indicators, research results or promotions. We understand percentage as being The reason between any number and 100, being represented by the % symbol. We use the idea of percentage to represent parts of something whole.
Read too: Calculation of percentage composition
Percentage representations

We know the percentage is one reason, soon, it can be represented by afraction, which, in turn, can be written in decimal form. In general, if we have a number accompanied by the % symbol, just divide it by 100, that is:

See the following examples that show the different representations of percentages. Remember, to “turn” the percentage into fraction, just divide the number accompanying the % symbol by 100 and simplify the fraction; to “transform” the fraction into decimal form, just perform the division.
Example
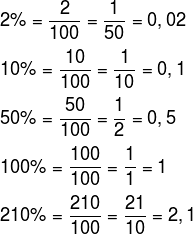
Note that when we write the percentage 100% it is the same as considering an integer, that is, when we consider
100% of something, we are taking into account the total of that. In the case of 210%, we are considering more than one integer, that is, we are considering 2.1 times the total.To make the way back, that is, given a fraction or a decimal number to be written in percentage form, just multiply the number in question per 100. Look:
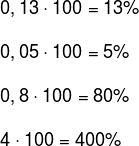
Read too: Percentage calculation with rule of three
Do not stop now... There's more after the advertising ;)
How to calculate the percentage?
To calculate the percentage of a value, just multiply this value by the percentage in its decimal or fractional form.
Example
- Calculate 50% of 600.
We know that 50% = 0.5, so just make the substitution and multiply the values. Look:
0,5. 600
300
It can also replace 50% in fractional form, leaving:
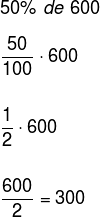
Hence, 50% of 600 = 300. See that 50% represents half of the total which is 600.
solved exercises
question 1 - (Enem) A person has invested a certain amount of money in the stock exchange. In the first month, she lost 30% of what she invested and, in the second month, she made a 40% profit on the balance that was left after the loss. After these two months, this person had with this investment, in relation to the initial capital applied,
- a loss of 2%.
- a profit of 2%.
- a loss of 4%.
- a 4% profit.
- the same amount of capital invested.
Solution
Let x be the amount that was invested in the stock exchange, as in the first month the person had a loss of 30% of this value, so we have to calculate this percentage in relation to the invested amount and then subtract from the amount. invested. Look:
30% of x
0,3. x
0.3x loss
So what was left on this person's account was:
x - 0.3x
0.7x
Since, then, the person had a 40% profit on the amount that was left over, we have to calculate this percentage on top of that amount and then add the result of this to the amount left over, having:
40% of 0.7x
0.4 · 0.7x
0.28x profit
So, we have that the remaining value is:
0.7x + 0.28x
0.98x
In relation to what was initially invested, the difference is:
x - 0.98x
0.02x
Thus, he had a loss of 2% in relation to the amount invested initially.
A:alternative to
question 2 - Calculate the value of (30%)2.
Solution
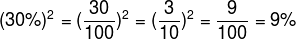
by Robson Luiz
Maths teacher



