Solve systemslinear it is a very recurrent task for studies in the fields of natural sciences and mathematics. The search for unknown values led to the development of methods for solving linear systems, such as the addition, equality and substitution method for systems that have two equations and two unknowns, and Crammer's rule and scaling, which solve linear systems of two equations, but which are more convenient for systems with more equations. A linear system is a set of two or more equations with one or more unknowns.
Read too:What is the relationship between matrices and linear systems?
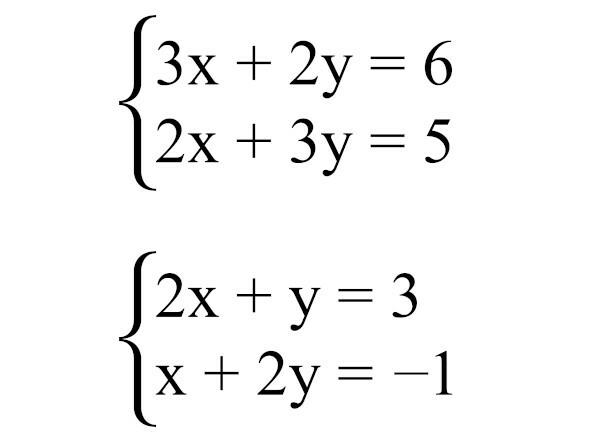
linear equation
The work with equations exists due to the need to find unknown unknown values. We call it an equation when we have an algebraic expression with equality, and it is classified as linear when the largest exponent of its unknowns is 1, as shown in the following examples:
2x + y = 7 → linear equation with two unknowns
a + 4 = -3 → linear equation with one unknown
Generally speaking, a linear equation can be described by:
The1x1 + the2x2 + a3x3... + anoxno = c
We know as an equation system when there is more than one linear equation. We will start with linear systems of two unknowns.
Do not stop now... There's more after the advertising ;)
Solving linear systems
Linear systems with two 1st degree equations and two unknowns
To solve a system of two equations and two unknowns, there are several methods, the three best known are:
- comparison method
- addition method
- substitution method
Any one of the three can solve a linear system of two equations and two unknowns. These methods are not as efficient for systems with more equations, as there are other specific methods to resolve them.
Replacement method
The replacement method consists of isolate one of the unknowns in one of the equations and perform the substitution in the other equation.
Example:

1st step: isolate one of the unknowns.
We call I the first equation and II the second equation. Analyzing the two, let's choose the unknown that is easiest to isolate. Note that in the equation I → x + 2y = 5, x has no coefficient, which makes it easier to isolate, so we'll rewrite equation I like this:
I → x + 2y = 5
I → x = 5 - 2y
2nd step: replace I in II.
Now that we have equation I with x alone, in equation II, we can replace x with 5 – 2y.
II → 3x – 5y = 4
Replacing x with 5 - 2y:
3 (5 - 2y) - 5y = 4
Now that the equation has only one unknown, it is possible to solve it to find the value of y.

Knowing the value of y, we will find the value of x by replacing the value of y in equation I.
I → x = 5 - 2y
x = 5 - 2 · 1
x = 5 - 2
x = 3
So the solution of the system is S = {3,1}.
Comparison method
The comparison method consists of isolate an unknown in the two equations and equalize these values.
Example:

1st step: let I be the first equation and II the second, let's isolate one of the unknowns in I and II. Choosing to isolate the unknown x, we have to:
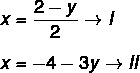
2nd step: equate the two new equations, since x = x.
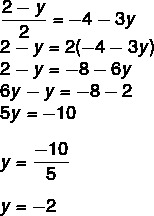
3rd step: replace the value of y by -2 in one of the equations.
x = -4 - 3y
x = -4 - 3 (-2)
x = -4 + 6
x = 2
So the solution of this system is the set S = {2,-2}.
See too: What are the differences between function and equation?
addition method
The method of addition consists in performing the multiplication of all the terms of one of the equations, in such a way that, when adding equation I to equation II, one of its unknowns is equal to zero.
Example:
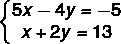
1st step: multiply one of the equations so that the coefficients are opposite.
Note that if we multiply equation II by 2, we have 4y in equation II and -4y in equation I, and that by we add I + II, we get 0y, so let's multiply all the terms in equation II by 2 so that this happen.
I → 5x – 4y = -5
2 · II → 2x + 4y = 26
2nd step: perform the sum I + 2 · II.
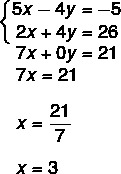
3rd step: replace the value of x = 3 into one of the equations.

Linear systems with three 1st degree equations and three unknowns
When the system has three unknowns, we adopt other solving methods. All these methods relate coefficients to matrices, and the most used methods are Crammer's rule or scaling. For the resolution in both methods, it is necessary the matrix representation of the system, including the 2x2 system can be represented by means of a matrix. There are two possible representations, the complete matrix and the incomplete matrix:
Example:
The system
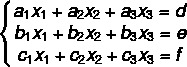
Can be represented by full matrix

And for incomplete matrix

Crammer's Rule
To find solutions for a 3x3 system, with unknowns x, y and z, using the Crammer's rule, it is necessary to calculate the determinant of the incomplete matrix and its variations. So we have to:
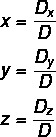
D → determinant of the incomplete matrix of the system.
Dx → determinant of the incomplete matrix of the system, replacing the column of x by the column of independent terms.
Dy → determinant of the incomplete matrix of the system, replacing the column of y by the column of independent terms.
Dz → determinant of the incomplete matrix of the system, replacing the column of z by the column of independent terms.
So, to find the value of your unknowns, we first need to calculate the determinant D, Dx, Dy associated with the system.
Example:
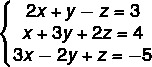
1st step: calculate D.

2nd step: calculate Dx.
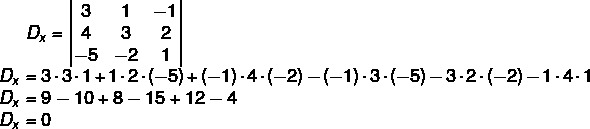
3rd step: then we can find the value of x, because:

4th step: calculate Dy.
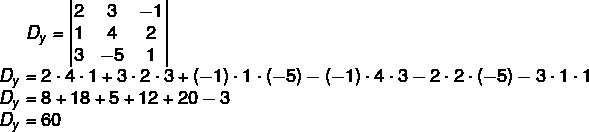
5th step: then we can calculate the value of y:
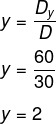
6th step: now that we know the value of x and y, in either line we can find the value of z by substituting the value of x and y and isolating z. Another option is to calculate Dz.
Substituting x = 0 and y = 2 in the first equation:
2x + y - z = 3
2 · 0 + 2 – z = 3
0 + 2 - z = 3
-z = 3 - 2
-z = -1 (-1)
z = -1
Therefore, the system solution is the tender (0.2,-1).
Also access: Problem solving by equation systems
scaling
Another method of solving linear systems is scaling, in which we only use the complete matrix and operations between the lines in order to isolate their unknowns. Let's scale the system below.

1st step: write the complete matrix that represents the system.

be L1, L2 and L3 respectively the lines 1, 2 and 3 of the matrix, we will perform operations between L1 and L2 and L1 and L3, so that the result makes the terms in the first column of the second and third row equal to zero.
Analyzing the second line of the matrix, let's replace it with the result of L2 → -2 · L1 + L2, in order to zero the term a21.
The21 = -2 · 1 + 2 = 0
The22 = -2 · 2 + 1 = -3
The23 = -2 · (-3) + 1 = 7
The24 =-2 · 10 + 3 = -17
So the L2 will be 0 -3 7 -17.
Analyzing the third row of the matrix, let's replace it with the result of L3 → 3L1 + L2, in order to reset the term to31.
The31 = 3 · 1 – 3 = 0
The32 = 3 · 2 + 2 = 8
The33 = 3 · (-3) +1 = -8
The34 = 3 · 10 – 6 = 24
So the L3 will be 0 8 -8 24.
Note that all are divisible by 8, so the L line3 keep it simple, let's divide it by 8.
L3 → L3 : 8 will be: 0 1-1 3.
So the new matrix of the scaled equation will be:
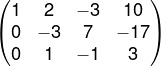
Now the goal is to reset column y in the third row, we will perform operations between L2 and L3, with the objective of resetting the second column of one of them.
We will replace L3 with L3 → L2 + 3L3.
The31 = 0 + 3 · 0 = 0
The32 = -3 + 3 · 1 = 0
The33 = 7 + 3 · (-1) = 4
The34 = -17 + 3 · 3 = -8
So L3 will be: 0 0 4 -8.
The new scaled matrix will be:

Now, when we represent this matrix as a system again, adding x, y, and z to the columns, we will find the following:
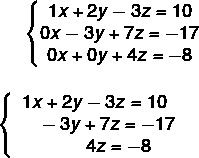
We can then find the value of each of the unknowns. Analyzing equation III, we have to:

If z = -2, let's substitute the value of z into the second equation:
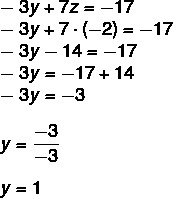
Finally, in the first equation, let's substitute the value of y and z to find the value of x.
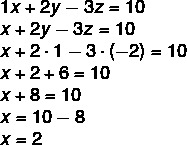
See too: 1st degree inequalities system – how to solve it?
linear system classification
A linear system is a set of linear equations, which can have several unknowns and several equations. There are several methods to solve it, regardless of the number of equations. there are three ratings for a linear system.
- Determined possible system (SPD): when you have a single solution.
- Undetermined possible system (SPI): when it has infinite solutions.
- impossible system(SI): when there is no solution.
solved exercises
question 1 (IFG 2019) Consider the sum of the measurements of a base and the height relative to that base of a triangle equal to 168 cm and the difference equal to 24 cm. It is correct to state that the measurements of the base and the height relative to this base measure, respectively:
a) 72 cm and 96 cm
b) 144 cm and 24 cm
c) 96 cm and 72 cm
d) 24 cm and 144 cm
Resolution
Alternative C.
Let h → height and b → base, then we have the following system:

By the method of addition, we have to:

To find the value of h, let's substitute b = 96 cm into the first equation:
b + h = 168
96 + h = 168
h = 168 - 96
h = 72 cm
question 2 The incomplete matrix that represents the following linear system is:
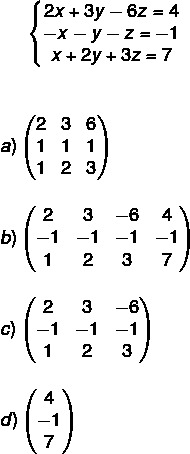
Resolution
Alternative C.
The incomplete matrix is one that has the coefficients of x, y and z, so it will be a 3x3 matrix. Analyzing the alternatives, the one that contains the 3x3 matrix with the correct signs is the letter C.
By Raul Rodrigues de Oliveira
Maths teacher


