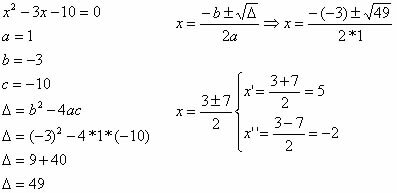One occupation high school, also known as occupationquadratic, is defined by the following rule:
y = f(x) = ax2 + bx + c
where a, b and c are real numbers and a ≠ 0.
As well as the first degree functions, at functionsquadratic can also have your graphic built. However, this is a more difficult task and depends on some prior knowledge, which will be discussed below.
Parable and its concavity
The graph of occupation of seconddegree is parable. The concavity of a parabola, which represents a function of the second degree, is defined by the numerical value of the coefficient. The in the role rule. If a > 0, the concavity of the parabola is turned upwards. If the
In the function f (x) = 2x2, notice that a = 2, which is a number greater than zero. Therefore, the concavity gives parable is facing up:

In the function g (x) = – 2x2, notice that a = – 2, which is a number less than zero. Therefore, the concavity gives parable is facing down.

vertex of a parabola
when a parable has concavity facing up, one of your points is lower than all the others. This point is called the vertex. When the parabola has a concavity facing downwards, one of its points is higher above all the others. This point is called the vertex.
Assuming that the vertex V of a parabola has the coordinates: V = (xvyv), to find their numerical value, we can use the following formulas:
xv = - B
2nd
yv = – Δ
4th
Where a, b and Δ are obtained from the coefficients of occupation. For example, in the function f(x) = x2 – 6x + 8, we will have the coordinates of V = (3, – 1), because:
xv = – (– 6)
2
xv = 6
2
xv = 3
for yv, we must calculate first:
Δ = b2 – 4·a·c
Δ = (– 6)2 – 4·1·(8)
Δ = 36 – 32
Δ = 4
Now we will use the formula for yv:
yv = – Δ
4th
yv = – 4
4
yv = – 1
Roots of a second degree function
the roots of a occupation are the domain values related to zero in the counterdomain. In other words, we set y or f(x) = 0 to find the values of x that make this statement true. the roots of a occupation they are also the meeting points of the graph of this function with the x axis.
Thus, the coordinates of the roots define the points A = (x’, 0) and B = (x’’, 0).
To find the roots gives occupation of seconddegree, you can use the Bhaskara's formula or any other method capable of computing roots of a function.
Example: As roots gives occupation f(x) = x2 – 6x + 8 are:
f(x) = x2 – 6x + 8
0 = x2 – 6x + 8
Δ = b2 – 4·a·c
Δ = (– 6)2 – 4·1·(8)
Δ= 36 – 32
Δ= 4
x = – b ± √Δ
2nd
x = – (– 6) ± √4
2
x = 6 ± 2
2
x’ = 6 + 2 = 8 = 4
2 2
x’’ = 6 – 2 = 4 = 2
2 2
S = {2,4}
And these roots are the two points of the function: A = (2.0) and B = (4.0)
Meeting point of the function with the y axis
The graph of a function is built in Cartesian plane. At functions of high school they always meet with the y axis of that plane at point (0,c). This means that the coordinate ç of the function is its meeting point with the y axis.
Second degree function graph
To build the graphic of a occupation of seconddegree, you will need to follow the step by step:
1st – Discover its concavity;
2nd – Find the coordinates of the vertex;
3rd – Find the coordinates of the roots of the function;
4th – Find two “random” points belonging to the function (if necessary).
Example: Let's build the graphic gives occupation f(x) = x2 – 6x + 8 using this step by step.
1st - A concavity gives parable is facing up since a = 1 > 0.
2nd – The coordinates of the vertex are: V = (3, – 1) and the procedures to find them are described above.
3rd – Find the roots gives occupation. Watch that some functions of the second degree will not have two distinct real roots. This happens when Δ = 0 or Δ graph.
So, in this example, we can already mark the points A, B and V, which are the roots and the vertex. O graphic of that occupation it will be:

4th – When the occupation it doesn't have two distinct real roots, look at the x coordinate of its vertex, choose x = xv + 1 and x = xv – 1, put these values in place of x in the function and find the y coordinate for them. Mark the two points obtained on the Cartesian plane, together with the vertex and draw the graphic.
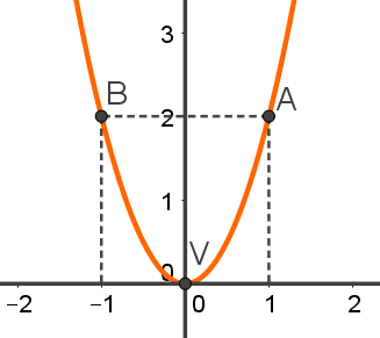
Example: Na occupation f (x) = 2x2, Δ = 0; xv = 0 and yv = 0. So, we will choose x = 1 and x = – 1 to calculate two other points that are not the roots and mark them in graphic.
f (x) = 2x2
f(1) = 2·12
f(1) = 2·1
f(1) = 2
f(–1) = 2·(–1)2
f(–1) = 2·1
f(- 1) = 2
So, points A and B of this occupation will be: A = (1, 2) and B = (– 1, 2), and your graph will be: