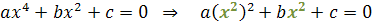One high school function is a rule that relates each element of a set to a single element of another and which can be reduced to the form: f (x) = ax2 + bx + c. O studyFromsignals of a function of the second degree is an analysis that determines the intervals of real numbers where the function is positive, negative, or null.
Central idea of the study of signals
When doing the studyFromsignals of a occupationofseconddegree, we are interested in finding out:
which numbers x belonging to the domain of this function make its y-image positive;
what values of x make y negative;
and which values of x cause y to be null.
Graphically, we are looking for intervals on the 0x axis where a occupation it's above the x-axis, below the x-axis, and over the x-axis. This means that we are looking for the respective intervals where the function is positive, negative or null.
Note the graphicgivesoccupation of seconddegree f(x) = x2 – 4x + 3:

In the graph above, for all x values greater than 1 and at the same time less than 3, the occupation is below the x-axis. Hence, the y values are negative. Also note that the function is above the x-axis for all x values greater than 3 and less than 1. In this way, the function is positive in these two intervals. The function is null at the meeting points between it and the x-axis, so in this case, exactly over points 1 and 3 of the x-axis.
That analyze can be used whenever the graphic of the occupation being available. When he's not there, you can use the methodalgebraic, which we describe below, or build the graphic gives occupation.
algebraic method
It is possible to perform the studyFromsignals of a occupation of seconddegree from its roots. Thus, the concavity of the parable which represents the function. For this, it is necessary to find the roots of the function of the second degree, by any method, and determine the concavity of the parabola that represents this function. This can be done by looking at the coefficient a:
If a > 0, the concavity of the parable is facing up.
If the parable is facing downwards.
in a given occupationofsecond degree f (x) = ax2 + bx + c, suppose your roots are x1 and x2.
If the coefficient a > 0, a concavitygivesparable is facing up. For this function, the range ]x1, x2[ causes the occupation be negative; values greater than x2 and smaller than x1 cause the occupation be positive if x2 > x1. Also, the x values themselves1 and x2 are the points where the function is null.
If the coefficient the parabola is turned down. Thus, the interval ]x1, x2[ causes the occupation be positive; values greater than x2 and smaller than x1 make the function negative, if x2 > x1. Also, the x values themselves1 and x2 are the points where the function is null.
Example:
Given the function f(x) = x2 – 4x, its roots are:
x2 – 4x = 0
x (x – 4) = 0
x = 0 or
x – 4 = 0
x = 4
Since a = 1 > 0, then, in the interval between 0 and 4, the function is negative. For any value greater than 4 or less than 0, the occupation is positive; and on points 0 and 4, this function is null.