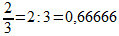Bi-squared equations are those that have degree 4, or equations of the 4th degree, whose exponents are even, as we will see later. Therefore, an indispensable condition is that there are no odd exponents in the equation to be solved.
Let's look at the general form of a bi-square equation:

Note that the unknown exponents are even exponents (four and two); this fact is important for us to carry out the steps of our resolution. If you are faced with an equation of the 4th degree that is not written in this way (only with even exponents), the steps we will use cannot be applied. Here is an example of a 4th degree equation that is not bisquare:
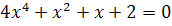
The expression we have to solve equations more easily is made only for 2nd equations. degree, so we must find a way to transform the bisquared equation into a 2nd equation. degree. For that, see a different way to write the equation:
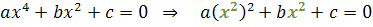
The unknown can be written so that the literal similar part (x²) appears. Starting from this, we will see the steps of solving a bi-squared equation.
1) Replace the unknown in the equation (in our example it is unknown x), x², by another unknown, that is, by another letter.
Make the following list: x2=y. With this you will be replacing the elements of the bi-squared equation in which x appears2, by the unknown y. As a result of this fact: x4=y2 and x2=y. See what our equation would look like:
Do not stop now... There's more after the advertising ;)

Thus, we have a 2nd degree equation, which has its own tools for its resolution. Root of a 2nd Degree Equation, High School Equation.
2) Obtain the solution set of the 2nd degree equation.
Remember that the solution set of this equation does not represent the solution of the bi-squared equation, as it refers to the equation in unknown y. However, the solution of this 2nd degree equation is of great importance for the next step.
3) According to the relationship made in the first step, x2=y, each solution of the unknown y equals the unknown x2. Therefore, we must calculate this relationship by substituting the roots of y for the equality x2=y.
Let's look at an example:
Find the roots of the following equation: x4 – 5x2 – 36 = 0
do x2=y. With that we will obtain an equation of the 2nd degree in the unknown y.

Solve this 2nd degree equation:
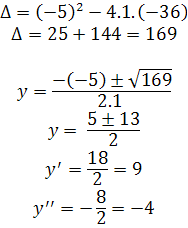
We must relate the two roots of the equation at Y, with the equation x2=y.
We have two values, so we're going to evaluate each root separately.
• y = 9;

• y = – 4;
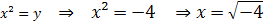
There is no value of x that belongs to the set of real numbers that satisfies the above equality, hence the roots (the solution set) of the equation x4 – 5x2 – 36 = 0 are the values x = 3 and x = –3.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Steps to Solving Bi-Square Equations"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/passos-para-solucionar-equacoes-biquadradas.htm. Accessed on June 28, 2021.