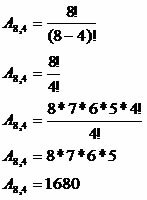Simple arrays of n elements taken p to p (p ≤ n) are the different ordered groupings that can be formed with p of the n given elements.
The total of these groups is indicated by An, p or Anp, which we calculate as follows:
An, p = n (n - 1)(n - 2) * ...*(n - p + 1) or
Examples:
A8.4 (where n = 8 and p = 4)
Simple Combinations
Simple combinations of n elements taken from p to p (p ≤ n) are the subsets with exactly p elements that can be formed from the n given elements.
It is indicated by Cn, p, Cnp the total number of combinations of n elements taken p a p
and calculated by C n, p =
(Note: As they are subsets, the order of the elements does not matter.)
Examples:
C6.2 (where n = 6 and p = 2)
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Simple Arrangements and Combinations"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/arranjos-e-combinacoes-simples.htm. Accessed on June 28, 2021.