Before checking which parts of a circle are, you remember which is the difference between circumference and circle?
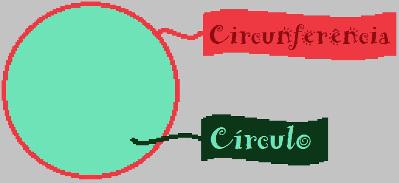
The circumference delimits the space filled by the circle.
When we see the image of a circular figure, like the one in the figure above, we can classify the circumference as the set of points that delimit the shape, the circle it is all the space inside the circumference.
Now that we've remembered the definition of a circle, let's identify all the parts that are present in it! Consider a circle whose center is a point. Ç and consider two points, THE and B, present at its end, that is, around its circumference:

Point C is at the center of the circle and points A and B are on the circumference.
If we make two straight segments, one that connects the points THE and Ç and another that calls C andB, the following figure will be formed:
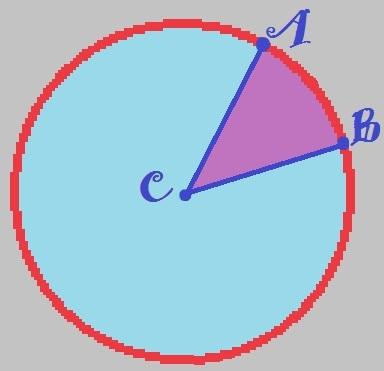
Line segments AC and BC delimit the minor circular sector (in purple) and the major circular sector (in blue).
The part colored in purple, which consists of the inside of the figure formed by the dots ABC, is called smaller circular sector. The blue part of the figure, formed by the circumference and the outside of ABC, is called larger circular sector.
not to forget: imagine that you have just taken a slice from a pizza. The removed slice represents the smaller circular sector, and what is left of the pie represents the larger circular sector.
Let's now draw a line segment to connect the points THE and B of the circumference:
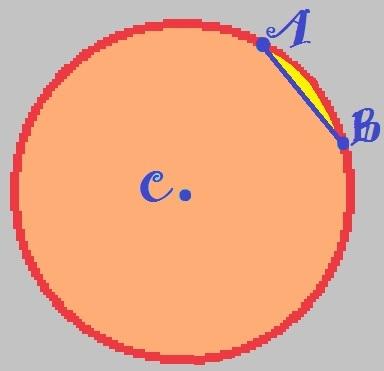
When tracing the ray AB, we find the major and minor circular segments.
When we draw the semi-straight AB, we segment the circle into two distinct parts. The smallest part, highlighted in yellow in the figure above, is called the smaller circular segment and does not contain the center of the circle. The larger part, which is orange, is called the larger circular segment and contains the center point of the circle.
not to forget: Imagine that you have dropped a plate on the floor and only a "edge" of the plate has broken. The broken part is the smaller circular segment and all that is left of the plate is the larger circular segment.
Let's now draw a line segment that passes through the point THE and by the point Ç of the circle, cutting the circumference at a point D:

A line segment that passes through A and C and intersects the circle at another point divides the circle into two semicircles.
When drawing a line segment that intersects the points THE and Ç and another point D of the circumference, there is the formation of two semicircles, which must be the same size. do you remember the elements of circumference? So you must remember that we can call the line AD in diameter!not to forget: a semicircle is always half a circle!
By Amanda Gonçalves
Graduated in Mathematics
Take the opportunity to check out our video lesson related to the subject:



