Some everyday situations related to Financial Mathematics involve the variation of commodity prices. Variations can occur in the direction of prices increase or decrease, occurring, respectively, inflation or deflation.
It is common in times of inflation the successive readjustment of prices, involving percentage indices. In case a certain product is continually readjusted, we have the incidence of several percentage indices on the original price. In this case, we say that the incidence of these indexes, successive times, is called the accumulated interest rate.
The accumulated interest rate of a given product is given by the following mathematical expression:
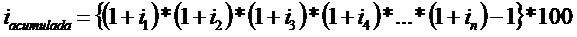
Example 1
Due to high inflation in successive months, the price of a product was readjusted in January, February, March and April by 5%, 8%, 12% and 7%, respectively. Determine the accumulated interest rate for those four months.
Turning percentage rates into unit rates:
5% = 5/100 = 0,05
8% = 8/100 = 0,08
12% = 12/100 = 0,12
7% = 7/100 = 0,07
Do not stop now... There's more after the advertising ;)
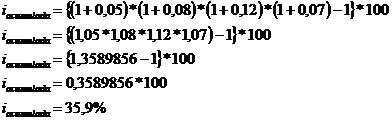
The interest rate accumulated in the four months was equivalent to 35.9% or, rounded up, 36%.
Example 2
When searching monthly for the price of a commodity, the following values were recorded on the last day of the month:
August: BRL 5.50
September: BRL 6.20
October: BRL 7.00
November: BRL 7.10
December: BRL 8.90
Determine the accumulated interest rate for the increase in the commodity in question.
Let's first calculate the increase rates. Look:

accrued rate

The accumulated rate of successive price increases for this commodity is equivalent to 61.79% or, rounded up, 62%.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Financial math - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Accumulated Interest Rate"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/taxa-juros-acumulada.htm. Accessed on June 29, 2021.