O equilateral triangle is a flat geometric figure whose main characteristic is the three congruent sides, that is, the measurement of these three sides is the same.
This fact generates an immediate consequence, the three angles The internals of this triangle are also equal to each other. Also, this triangle it has important geometric properties that facilitate the resolution of certain problem situations.
Read too: What is the condition of existence of a triangle?
Properties of equilateral triangles
The equilateral triangle has some properties that facilitate the resolution of some problem situations.
Property 1 – All internal angles of an equilateral triangle measure 60°.
Property 2 – The height (segment perpendicular to one of the sides), median (segment that divides one side in half) and bisector (segment that divides an angle in half) coincide.
Perimeter of the equilateral triangle
We know that the perimeter of a polygon any is given by sum of measurements from all sides, and in the equilateral triangle, the idea is no different. Because the equilateral triangle has all sides equal, we can find a formula that makes it easier to calculate the perimeter.
Consider an equilateral triangle of side l:
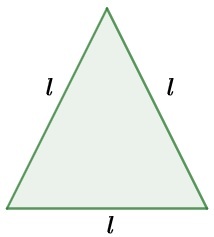
As the perimeter is given by the sum of all sides, then:
2P = l + l + l
2P = 3 · l
Remember: the perimeter notation is 2P. We use the letter P to represent the semiperimeter. The formula states that to calculate the perimeter of an equilateral triangle just multiply the side measurement by 3.
- Example
Determine the perimeter of the equilateral triangle whose side is 4 cm.
Substituting the value of the side in the deduced formula, we have:
2P = 3 · l
2P = 3 · 4
2P = 12 cm
So the perimeter is 12 centimeters.
Read too: Similarity of triangles: what are the cases?
equilateral triangle area
To calculate the area of an equilateral triangle, we initially plot the height relative to one of its sides. From the properties we know that the height coincides with the median, that is, when plotting the height, the side is divided in half.

We know that the area of any triangle is given by the multiplication of base with height, and that divided by 2.
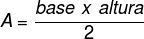
Note that the base value is known in case 1, however the height value is unknown. Thus, to determine the area of the equilateral triangle, it is first necessary to find its height. For this, we will use the Pythagorean theorem:

Since we now know the height measurement, we can substitute it into the formula for the area of a triangle.
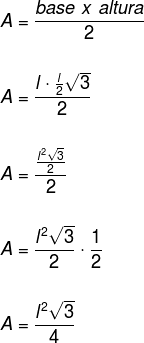
Example
Determine the area of the equilateral triangle whose side measures 4 cm.
To calculate the area of an equilateral triangle, simply substitute the measure of the side in the formula, knowing that in the formula l represents that measure. So we have:


solved exercises
question 1 – A farmer had to build a pen so his chicken farm wouldn't run away. When making the project, he noticed that the enclosure would be in the form of an equilateral triangle with a length of 3 meters on one side. How many meters of fence will this farmer have to buy? Knowing that each meter costs 4 reais and 50 cents, how much will he spend?
Resolution
The farmer's terrain can be represented by:

The perimeter is given by:
2P = 3 · 3
2P = 9m
As each meter costs 4.50 reais, the farmer will spend 9 times this amount:
spent = 4.5 · 9
spent = 40.5
Therefore, the farmer will spend 40 reais and 50 cents.
question 2 – A tile company needs to cover the bottom of a pool with 1 m tiles2. The pool is shaped like a 6 meter equilateral triangle. Determine the amount of tiles to be used.
(Given: Use √3 = 1.7)
Resolution
We initially determined the pool area.

As each tile is 1 m2, then 16 tiles will have to be purchased, since 0.3 tile is not sold.



