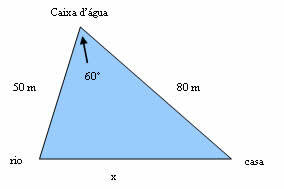
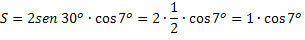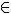Inside of numerical sets there are the whole numbers, which are characterized by the existence of positive and negative numbers. You can probably quickly answer what is the result of 2 + 3 or of 7 – 1, but what about the addition and the subtraction of negative numbers? Do you know how to calculate (– 2) + (– 3) or (– 7) – (– 1)? If you don't know or even have any doubts, we'll take you step by step to resolve these and other examples.
We will perform these calculations using a numbered line. Regardless of the calculation, we will always start from ZERO. Let's see the cases that may appear:
if the number is positive, we will walk the number of houses indicated for the right (→);
if the number is negative, we will walk to the left (←);
If we're doing integer subtraction, we're going the other way around;
If it's an addition of whole numbers, it won't change anything!
It may sound complicated, but in practice it is very simple! Let's look at some examples:
1st Example: (–2) + (–3)
Leaving zero, we will walk two spaces to the left, stopping at – 2.
We will then walk another three houses to the left, stopping at – 5.Then, (– 2) + (– 3) = – 5.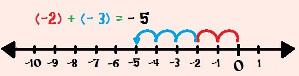
Calculating (– 2) + (– 3) with the help of the number line
2nd Example: (– 7) – (– 1)
Leaving zero, we will walk seven spaces to the left, stopping at – 7. We should walk one house to the left, but since it's a subtraction, we reverse side and walk one house to the right, stopping at – 6.Soon, (– 7) -- (– 1) = – 6.

Calculating (– 7) – (– 1) with the help of the number line
3rd Example: (– 1) + (+ 4)
Leaving zero, we will walk one house to the left, stopping at – 1. We will then walk another four houses to the left, stopping at + 3.Then, (– 1) + (+ 4) = 3.
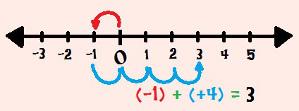
Calculating (– 1) + (+ 4) with the help of the number line
4th Example: (+ 3) – (– 2)
Leaving zero, we will walk three spaces to the right, stopping at +3. We should walk two houses to the left, but since it's a subtraction, we reverse side and walk two houses to the right, stopping at + 5.Then, (+ 3) – (– 2) = 5

Calculating (+ 3) – (– 2) with the help of the number line
5th Example: (– 2) + (+ 3) – (+ 5)
Leaving zero, we will walk two spaces to the left, arriving at the – 2. We will then walk three houses to the right, stopping at + 1.We should walk five houses to the right, but since it's a subtraction, we reversed the side and walked five houses to the left, stopping at – 4.Then, (– 2) + (+ 3) – (+ 5) = – 4.
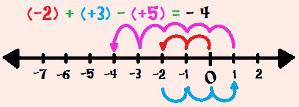
Calculating (– 2) + (+ 3) – (+ 5) with the help of the number line
6th Example: (+1) – (+ 3) + (–6)
Starting from zero, we will walk one house to the right, arriving at the + 1. Then we should walk three squares to the right, but since it's a subtraction, we reverse side and walk three houses to the left, stopping at – 2.Finally, we walked another six houses to the left, arriving at the – 8.Then, (+ 1) – (+ 3) + (– 6) = – 8.

Calculating (+1) – (+ 3) + (– 6) with the help of the number line
By Amanda Gonçalves
Graduated in Mathematics