We all have some idea of what a straight line is: a line that doesn't curve at all. When this straight line is cut anywhere along its length, we call the two parts formed semi-straight lines. Since the lines are infinite for either side, these two parts of the cut made on the line have a starting point and an ending point. If a second cut is made in any of the ray lines, the figure formed will also have a starting point and an ending point, configuring what we know as a straight line segment.
When joining straight segments, one of the figures formed is known as polygon.
To be a polygon, the geometric figure must meet the following conditions:
1- The straight segments must be connected by their ends, so that they form a single line;
2- Line segments cannot cross;
3- the figure must be closed, that is, all line segments must meet other segments at their start and end points.

In the image above, figures A, B and C meet all the prerequisites to be considered polygons. Figure D, on the other hand, is open and figure E has two intersecting straight lines, so they are not polygons.
Another important feature of polygons is whether or not they are convex. This definition is important because of the existence of the polygon's internal angles. A convex polygon will always have interior angles less than 180°. The same cannot be said for a non-convex polygon.
convex polygon is the one in which, by marking two points inside it, the connection between these two points will always be totally inside the polygon, regardless of the location chosen for the two points.
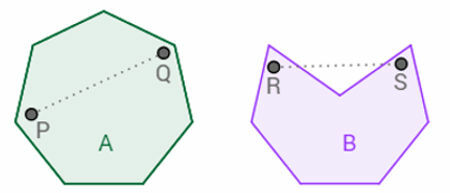
The image above shows a polygon A where, regardless of the location of points P and Q, the segment PQ will always be completely inside the polygon. Polygon B, on the other hand, offers many options to draw a line segment with a piece outside the polygon, such as the R and S points chosen inside it. A is an example of a convex polygon and B is an example of a non-convex polygon. The impression one gets when looking at a non-convex polygon is that it has an entrance similar to a “mouth”.
Every convex polygon has the following elements:
1- Sides: each line segment that makes up the polygon;
2- Inner angles: angles between two consecutive straight segments within the polygon;
3- External angles: These are the angles on the outside of the polygon formed by the extension of an internal angle. The sum between the inner angle and its extension (outer angle) will always be 180°;
4- Vertices: These are the meeting points between two consecutive sides;
5- Diagonals: All line segments resulting from the connection between two non-consecutive vertices of a polygon.

The polygon in the image above has all these elements represented. Segment AB is an example of a side; the 128.57° angle is an example of an internal angle; the 51.43° angle is an example of an external angle; point A is an example of a vertex; and any dotted segment within the polygon is an example of a diagonal.
By Luiz Paulo Moreira
Graduated in Mathematics
Take the opportunity to check out our video classes on the subject: