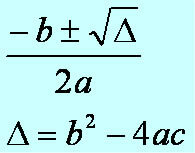One angle is the measure of the gap between two semi-straight from the same origin (same starting point). Note the four angles in the figure below:

Note that the angles α and β are on the line r and have one side in common. Angles γ and β are on the line s and they also have one side in common. Angles γ and α are not on it straight, and the only point they have in common is vertex O.
In this case, we say that the angles α and β are adjacent, and the angles γ and α are oppositesfurvertex. Doing a similar analysis, we will find all pairs of adjacent angles:
α and β
γ and β
γ and δ
δ and α
The pairs of angles opposed by the vertex are as follows:
α and γ
β and δ
properties
At a crossing of two straights, anglesadjacent they are supplementary.
are not any anglesadjacent which are supplementary, only when there is a meeting between two straight. Remembering that supplementary angles are those whose sum is equal to 180°.

Thus, in the figure above, it will always be true that:
α + β = 180°
γ + β = 180°
γ + δ = 180°
δ + α = 180°
At an intersection of two straight lines, angles opposed by the vertex are congruent.
Remember that two angles are congruent when they are distinct but have the same measurement.
Thus, in the previous figure, it is always true that:
α = γ
β = δ
Notice that anglesadjacent they are always supplementary, as they form “the angle of a straight line”, which is 180°. Now consider the adjacent angles:
α + β = 180°
γ + β = 180°
Note that both sums result in the same value, so we can write:
α + β = γ + β
α = γ + β –β
α = γ + 0
α = γ (are oppositesfurvertex)
Examples
1º) In the image below, calculate the measure of each angle.

Note that γ = 60°, as they are oppositesfurvertex. In addition, γ + β = 180°, therefore:
γ + β = 180°
60° + β = 180°
β = 180° – 60°
β = 120°
Note, finally, that δ = 120°, as it is oppositefurvertex to β.
2º) Calculate the value of each highlighted angle:
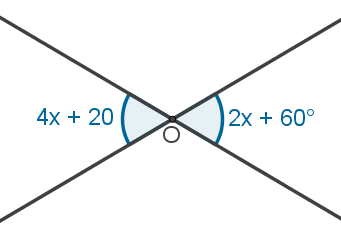
How the highlighted angles are oppositesfurvertex, we can write:
4x + 20 = 2x + 60
4x - 2x = 60 - 20
2x = 40
x = 40
2
x = 20
So each angle measures:
4x + 20 = 4·20 + 20 = 80 + 20 = 100°
By Luiz Paulo Moreira
Graduated in Mathematics
Related video lessons: