O triangle isosceles has as main feature twosidescongruent, that is, it has two equal sides. This implies the presence of two congruent interior angles, and they are called base angles. for being a flat figure, let's determine an expression that allows us to calculate its area.
Read too: What is the condition of existence of a triangle?
Property of isosceles triangles
Consider the isosceles triangle ABC.
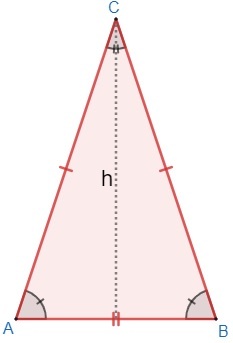
At the triangle, see which sides AC and BC are congruent. O angle opposite these sides, AB, is incongruous and called base angle or base of the right triangle.
Another important property of isosceles triangles is the coincidence of height and median relative to the base of the triangle, that is, the line segment perpendicular to the base of the triangle and the line segment that divides that base are equal.
Note that this line segment divides the isosceles triangle exactly in half, for this fact, this segment is also called the symmetry axis.
Read too: Triangle classification - criteria and names
isosceles triangle area
It is known that the area of any triangle is given by the following formula:

In general, in isosceles triangles area calculation problems, just find the height using the Pythagorean theorem.
To find the area of a triangle isosceles, let's consider the following example.
Example
Determine the area of the following triangle:
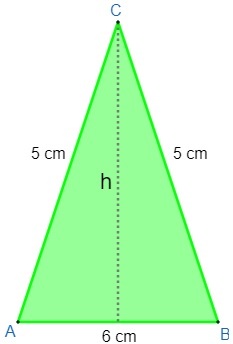
Note that triangle ABC is isosceles because it has two equal sides. Also see that height split the isosceles triangle in two. So let's find the height and substitute it in the formula. Remember that the height coincides with the median, that is, it divides side AB in half.
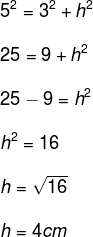
Replacing the height value in the formula, we have:


Exercise solved
question 1 – It is known that, in an isosceles triangle, the internal angle opposite the base measures 30°. Determine the measurement of the base angles.
Resolution
Let's build an isosceles triangle to make the resolution easier, remember that the base angles are equal, so we can represent them with the same letter.
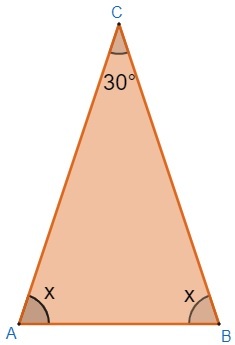
We also know that the sum of the internal angles of a triangle is 180°, so:
x + x + 30° = 180°
2x = 180° - 30°
2x = 150
x = 150° ÷ 2
x = 75°