Albert Girard (1590 – 1633) was a Belgian mathematician who established relations of sum and product between the roots of a 2nd degree equation. Around the 17th century, numerous western mathematicians developed studies in order to establish relationships between the roots and coefficients of a quadratic equation. The big obstacle was the presence of negative numbers as a result of the roots, which was not accepted among scholars. It was Girard who developed a method capable of determining relationships using negative numbers. Let's look at the following demonstrations, responsible for the expressions of the sum and the product of the roots of a 2nd degree equation.
We have that an equation of the 2nd degree has the following form: ax² + bx + x = 0. In this expression, we have that the coefficients a, b and ç are real numbers, with to ≠ 0. The roots of a 2nd degree equation, according to the solving expression are:

sum between the roots
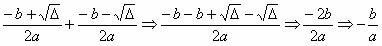
Product between the roots
Do not stop now... There's more after the advertising ;)
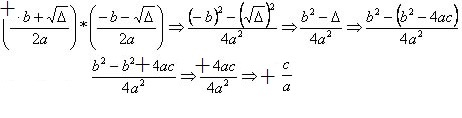
Example 1
Let's determine the sum of the roots of the following 2nd degree equation: x² - 8x + 15 = 0.
Sum
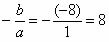
Product
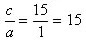
Girard relations are not just for determining the sum and product of roots. They are tools used to compose 2nd degree equations. Equations are represented by: x² - Sx + P = 0, where S (sum) and P (product).
Example 2
Determine the 2nd degree equation, with a = 1, which has as roots the numbers 2 and – 5.
Sum
Y = x1 + x2 → 2 + (–5) → 2 – 5 → – 3
Product
P = x1 * x2 → 2 * (–5) → – 10
x² - Sx + P = 0
x² – (–3)x + (–10)
x² + 3x – 10 = 0
The equation sought is x² + 3x – 10 = 0.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Equation - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Studying Girard's Relationships"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/estudando-as-relacoes-girard.htm. Accessed on June 29, 2021.

