O set of irrational numbers is formed by the numbers that cannot be represented as fractions. In some situations, the set of rational numbers was not enough to solve problems, that's when the existence of irrational numbers was noticed, such as the inexact roots, the non-periodic tithes,the π, between others.
Read too: What is the value of a digit?
Set of irrational numbers
Throughout history, in the application of Pythagorean theorem in a right triangle of sides measuring 1, the answer was found to be equal to the root of the number 2.

It turns out that this seemingly simple answer made it possible to discover a new numeric set. In an attempt to find the answer to this source square of 2, found one decimal number known as non-periodic tithe, what is impossible to be represented as a fraction. This made it necessary to create a new set, the irrationals, since, until that moment, all numbers were rational (which can be written as a fraction).
The set of irrational numbers is composed of all numbers that no can be written in the form of a fraction. |
What are irrational numbers?
For a number to be considered irrational, it must respect the definition, that is, it cannot be represented as a fraction. These numbers are the inexact roots, at non-periodic tithes and some special cases, such as the constant π (read: pi) or the number ɸ (read: fi), among others.
Roots not exact
When the number is not a perfect square, it is known as a non-exact root. See some examples:

non-periodic tithes
When solving these roots, the answer will always be an approximation, what we call non-periodic tithes.
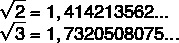
Note that the decimal part is infinite and that there is no period, that is, a sequence that causes the we can predict the next number in the decimal part, and that's why we call this number a decimal not periodic. Not only the decimals generated by inexact roots, but any non-periodic decimal is an irrational number.
other irrational numbers
• Number π: is quite common for calculations involving curves such as area and length of circumference or volume of cylinders and cones, and is one of the best known irrational numbers. Because it is irrational, we use a symbol to represent it, yet π is a non-periodic decimal, it's yours value is equal to 3.14159265358979323846… Several places of this number are known, but we normally use an approximation, with the value of 3.14.
• Number ɸ: is also known as golden number and it has been studied since Antiquity, describing various natural phenomena, such as the reproduction of rabbit populations. There is also a report on the use of this proportion in artistic works. It is also an irrational number, and so it is represented by the symbol ɸ, its value being: 1.61803398875…
• Euler's constant: is used for phenomena involving financial math, and in the areas of biology, astronomy, among others. It is also an irrational number and therefore is represented by the symbol and, with a value of: 2.718281828459045235360…
See too: Prime numbers - natural number that has only two dividers
rational and irrational number
It turns out that any number can be classified as rational or irrational. Directly, O rational number is every number that can be written as a fraction. Exact decimals, periodic decimals, whole numbers are rational numbers. The irrational numbers, on the other hand, are the opposite of that, that is, they are those that cannot be written as a fraction, as we mentioned, they are non-periodic decimals and non-exact roots.
- Example
The tithe 3.12121212... is periodic, note that in its decimal part there is a period, which is the number 12, which is always repeated, therefore, this number is rational.
The 6,1249375 tithe…. is non-periodic, note that there is no period in its decimal part, which makes this number irrational.

solved exercises
Question 1 - Which of the following numbers can be classified as irrational?

Resolution
Alternative C.
a) We know that 25 is a perfect square, that is, its square root is exactly equal to 5, so this is a rational number.
b) When calculating the root of 81, we know that its result is 9, which makes that number rational.
c) 10 does not have an exact square root, that is, it is an irrational number, which makes alternative C correct.
d) 5.1888 is an exact decimal number, so it is rational.
e) 1.2323… is a tenth with a period equal to 23, so it is a rational number.
Question 2 - About irrational numbers, judge the following statements as true or false:
I - Every square root is an irrational number.
II - Every non-periodic decimal is an irrational number.
III - The number ɸ and the number π are examples of irrational numbers.
According to the judgment of the sentences, it is correct to state that:
a) Only statement I is true.
b) Only statement II is true.
c) Only statements II and III are true.
d) Only statements I and II are true.
e) All statements are true.
Resolution
Alternative C.
I - False, as only the non-exact square root is an irrational number.
II - True. Non-periodic decimals are irrational numbers.
III - True, since the numbers ɸ and π are non-periodic decimals, therefore, they are irrational numbers.