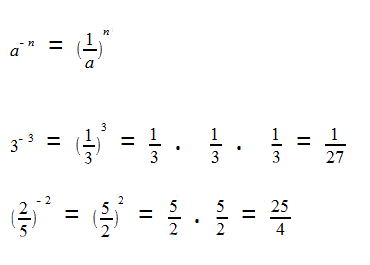O cylinder volume is calculated by multiplying the base area and the height. As the base is a circle, we use the formula of the area of a circle times the height of that cylinder. The cylinder is a geometric figure formed by two circular bases and a lateral area that connects these two circles.
This form is quite common in everyday life, seen in soda cans and oxygen cylinders, among other objects. Calculating the volume of the cylinder is to calculate the space it occupies and also its capacity, for example, to know the quantity of ml in the soda can.
The cylinder is a very common object also in laboratories for chemical experiments where the volume is of great importance, for example, to calculate the density of an object, we need its volume.
Read too: Cone – geometric solid that also has a circle as its base

Cylinder volume formula
To know the volume of a cylinder, we need to calculate the product
enter the base area AB and the height h from it, however, when we analyze the figure, we know that its base is a circle. THE area of a circle of radius r is calculated by formula Acircle = π r², which justifies the formula to calculate the volume of the cylinder: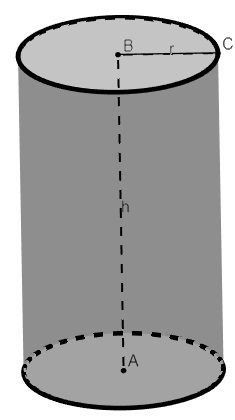
| Vcylinder = π · r² · h |
h → height
r → base radius
How to calculate cylinder volume?
In order to be able to apply the formula, we need the height and radius value of the cylinder, then we perform the radius and height value substitutions and, when necessary, we use an approximation of the value of π.
Example 1:
Calculate the volume of the following cylinder (use π = 3.1):
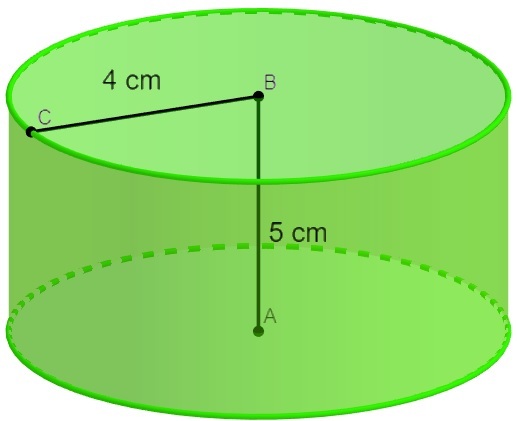
To calculate the volume, we have r = 4 and h = 5, so, performing the substitutions, we have to:
V = π · r² · h
V = 3.1 · 4² · 5
V = 3.1 · 16 · 5
V = 3.1 · 80 = 248 cm³
See too: How to calculate the total area of the cylinder?
solved exercises
Question 1 - Marta is renovating her house and has decided to change the water tank. This new water tank has a cylindrical shape. Knowing that the dimensions of the chosen box are 1.20 meters in diameter and 5.40 meters in height, and knowing that after 12 hours, it will have half its volume filled, what will be the amount, in liters, of water that will be in the box in this time? (Hint: 1 m³ = 1000 liters and use π = 3.)
a) 8748
b) 2916
c) 23328
d) 11664
e) 5832
Resolution
Alternative B
Since the diameter d = 1.20, we know that the radius is half the diameter, that is, r = 0.60 meters.
V = π · r² · h
V = 3 · 0.6² · 5.4
V = 3 · 0.36 · 5.4
V = 5.832 m³
Multiplying by 1000, to convert to liters, we have to:
5,832 · 1000 = 5832 liters
This is the total volume, as we want half, just divide 5832 by 2.
5832: 2 = 2916 liters
Question 2 - A fuel transport truck has a tank in the shape of a cylinder as shown in the image below:

When analyzing the reservoir cylinder, it was found that the radius of the reservoir is equal to 2 meters, remembering that in 1 m³ 1000 liters can fit, which should be the minimum height of this cylinder for the truck to be able to transport 54,000 liters of fuel? (Use π = 3.)
a) 5 meters
b) 4.5 meters
c) 9 meters
d) 3.5 meters
e) 7 meters
Resolution
Alternative B
We know that the volume V has to be equal to 54,000 liters and that each 1 m³ = 1000 liters, so the reservoir needs to have 54 m³.
Then:
V = 54 m³
π · r² · h = 54
Given π = 3 and r = 2, then:
3 · 2² · h = 54
3 · 4 · h = 54
12 · h = 54
h = 54: 12
h = 4.5 meters