In the theory of odds, an event is a subset of sample space. This means that the event is formed by a set of possible outcomes of a random experiment, therefore, it can have from none to all the elements of the space to which it belongs.
already one complementary event is formed as follows: If we consider And a event, it is part of a subset of spacesample Ω. The set of elements belonging to Ω that are not present in E constitutes a subset known as complementary event of E. This can be demonstrated as follows:
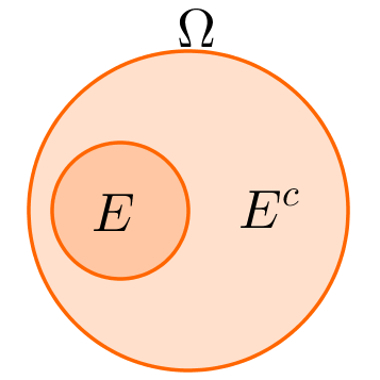
In the image above, E is a event any and Eç is the complementary event of E.
Example: Consider throwing a die a random experiment in which possible results can be seen on its upper face. Then imagine that the event "leaving a composite number" can be represented by the following set:
E = {4, 6}
In this case, the eventcomplementaryof E (ANDç) is the set:
ANDç = {1, 2, 3, 5}
That's because the eventcomplementary of E is the set formed by all the elements of the sample space that do not belong to E. In this example, therefore, if the number of elements of the event n (E) is two, the number of elements of the complementary event n (Eç) will equal four.
Calculating the probability of a complementary event
There are two ways to calculate the probability of occurrence of a eventcomplementary:
Calculate the probability of the event occurring and then decrease the obtained number by 100% (or decrease it by one, if there are decimal numbers instead of percentages);
Calculate the number of elements of the complementary event and calculate normally the probability occurrence of this event.
Example: Calculate the probability that, on the roll of a die, the top face is not a composite number.
FOOTç) = 1 - P(E)
FOOTç) = 1 – huh)
n (Ω)
FOOTç) = 1 – 2
6
FOOTç) = 1 – 0,3333…
FOOTç) = 0,6666…
FOOTç) = 66.6% approximately.
Another way to calculate this probability:
FOOTç) = huhç)
n (Ω)
FOOTç) = 4
6
FOOTç) = 0,66…
FOOTç) = 66.6% approximately.
Note that the result of both forms of calculation is the same. There are cases where it is easier to use the first form of calculation, and others where it is easier to use the second.
Relationship between an event and its complement
If we consider E an event and Eç its complement, the possible relationship between them can be represented as follows:
AND∩ANDç = Ø
ME ANDç = Ω
This relationship can be understood as follows: the intersection between an event and its complementary event will always be an empty set. This is because the two will never be able to share elements (possible results). The union between an event and its complementary event will always result in the sample space, that is, together, these two sets contain all of the possibilities.
By Luiz Paulo Moreira
Graduated in Mathematics
Related video lesson: