You triangles are flat geometric figures formed only by straight segments, closed and that they have only three sides. There is a property about these sides, known as the condition of existence of a triangle, which determines whether a triangle it may or may not exist according to the length of its sides. This property will be studied below.
Foundation of the condition of existence
imagine that a triangle will be constructed with three fixed-size rods. The largest one will be placed horizontally. Look the following picture:
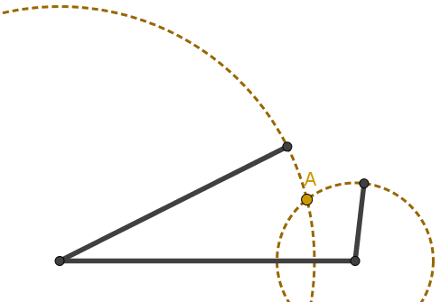
Construction of a triangle with fixed measures for the sides
Note in the image below that, if we rotate the two sticks, they will touch each other at point A, closing the triangle.
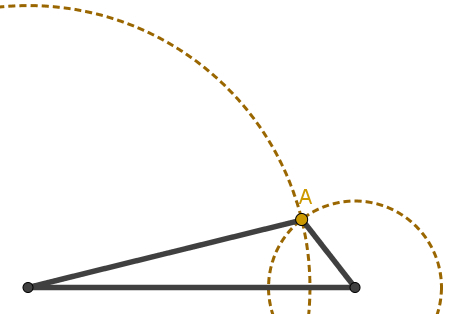
In the image below, observe from the trajectory that the rods will not touch, regardless of the turn you make with them.

Note that there is a property around the length of the sides of the triangle so that it is possible to build it. This property is what we call the condition of existence of a triangle.
condition of existence
The condition for these rods to touch is the following: the result of the sum of the measurements of the two rods that were rotated must be greater than the measure of the horizontal rod. Translating it into mathematical language, we will have the following rule:
In any triangle, the sum of the measures of two sides is always greater than the measure of the third.
Looking at the images above, these sides being added are the free rods that have been rotated. Note that the length of the rods is just the circle radius which describes the possible trajectory of its extremities. So, for there to be triangle, there must be an intersection point between these circles.
Just note that this point cannot be tangency, that is, these circles cannot touch at just one point, because, in this way, the sum of the two free sides of the triangle would be equal to the measurement of the third. With that, we would have the following figure:
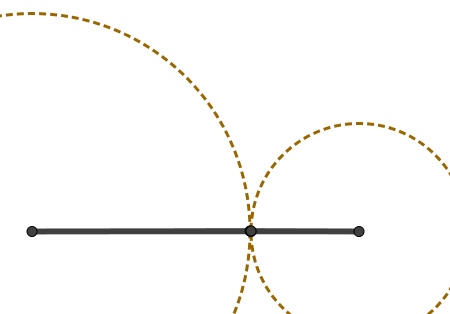
This figure, of course, is not a triangle.
Suppose the measurements of the sides of a triangle are The, B and ç. The condition of existence of a triangle is as follows:
The
B
ç
This condition is also known as inequalitytriangular. However, it is not necessary to check all of them to ensure the existence of a triangle. Whenever the sum of the two smallest sides of a triangle is greater than the length of the longest side, that triangle is possible.
To better understand, imagine that The is the largest measure among the three. So if
The
B will be less than a + c and ç will be less than a + b.
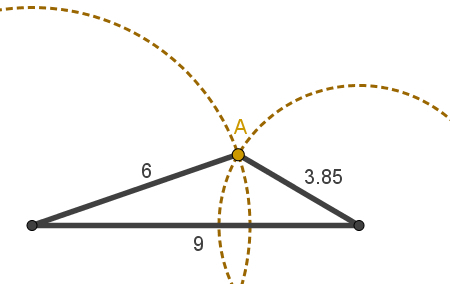
Triangle in which the inequalities mentioned above apply
Note that the triangle of the image above obeys this rule. 9
By Luiz Paulo Moreira
Graduated in Mathematics



