Imagine the following situation: you want to buy a toy that costs R$25.00. For that, you break your piggy, but the money is not enough, you only have R$ 19.00. If so, what would you do to buy the toy? The most practical idea is to look for someone who has more money and can lend. Imagine that a friend has $20.00 and he decides to lend you the money. He lends you BRL 6.00, which is what you need, and still keeps BRL 14.00.
In mathematics, when we need to subtract a value and we can't, we can “borrow”, a practice also known as subtraction with reservation. Before doing subtraction examples with reservations, let's recall a very important idea:
1 ten = 10 units
1 hundred = 10 tens
1 unit of thousands = 10 hundreds
Whenever an order needs to lend something to another order, it cannot lend more than one, that is, the dozens can lend 1 ten for units, hundreds can lend 1 hundred for the tens and so on.
Now we are ready to solve some examples:
First let's try to do: 357 - 139
c | d | u
3 5 7
– 1 3 9
We must start the subtraction at the end, in the order of the units. But we couldn't take 9 units out of just 7. At this point, the seven needs to borrow a ten from its neighbor to the left, so the five tens becomes just four, and a ten will join the units. But, as we speak, 1 ten = 10 units. So, if we already had 7 units, now we will have 17.
c | d | u
3 417
– 1 3 9
2 1 8
Now we've finished solving the subtraction, see the step by step:

See the 357 by 139 subtraction step by step
Let's now do the following subtraction: 731 – 699:
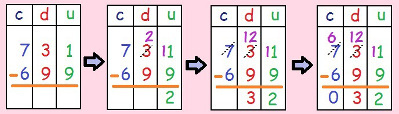
See step by step the subtraction of 731 by 699
In the diagram above, we see that, in the order of the units, we have the subtraction 1 – 9. To be able to solve it, we must borrow a dozen from the number to the left of 1. In the tens place, there were 3 dozen and only two will remain. In the units, we now have the following calculation: 11 – 9 = 2. In the dozens, we have 2 – 9,therefore, to subtract, we first need to take a hundred in the left house, leaving only six hundred left. Already in the dozens, we now have: 12 – 9 = 3. To finish the bill, we'll do it in the hundreds: 6 – 6 = 0. Therefore, 731 – 699 = 32. Try doing some subtractions with reservations and tell us the results!
135 – 129 =
278 – 199 =
1.257 – 987 =
By Amanda Gonçalves
Graduated in Mathematics