Coordinates of the vertex of the parabola

At high school functions can be represented in the Cartesian plane through parables. O vertexinoneparable it is its highest point when its concavity is facing downwards, or it is its lowest point when its concavity is facing upwards. as we are talking about functions on the Cartesian plane, we can think of coordinates of the vertex of the parabola, which are given by the following equations:

x_v = - B
2nd

y_v = – Δ
4th

In these formulas, x_v and y_v are the coordinatesofvertex V(x_vy_v). In addition to these two ways, there is also a method that makes use of roots of the function to find the coordinates of the vertex. This method can also be used to demonstrate these formulas.

Roots method

To find the coordinatesofvertex of a parable, based on this figure on the Cartesian plane or on the function that represents it, we can use a method based on its roots, which consists of doing the following:

1 - Determine the roots x₁ and x₂ gives occupation;

2 – Find the midpoint of the segment whose ends are the x-roots₁ and x₂. That Scoreaverage it's just the x coordinate_v from the vertex.

3 – Find the value of occupation at point x_v, that is, calculate f(x_v) results in the y-coordinate value_v from the vertex.

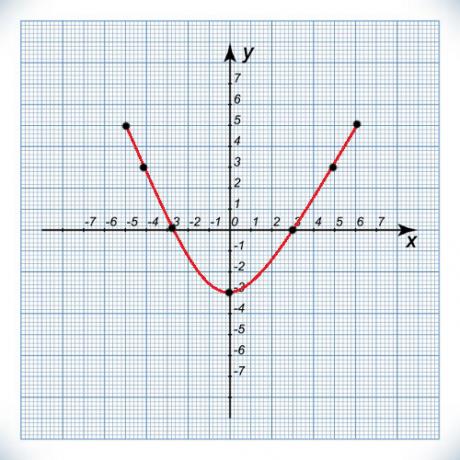
Example: Note the parable of the figure below, which represents the occupation f(x) = x² – 16.

Knowing that the roots of a function are the values ​​of x that make f(x) = 0, then the roots of that function parable are 4 and – 4. The midpoint of segment AB, whose ends are the roots, is precisely the point C whose x coordinate coincides with the coordinate x_v of vertex. This rule is valid for every parable that has roots.

To find the coordinate y_v of vertex, we must calculate f(x_v):

f(x) = x² – 16

y_v = f(x_v) = (x_v)² – 16

y_v = (0)² – 16

y_v = – 16

Observing the graph, we can see that this value obtained coincides with the coordinate y_v of vertex.

This calculation can always be done when the occupationofseconddegree it has roots. To know if a second degree function has roots, it is enough to assess the value of its discriminating. If it is not negative, the function has roots. For this calculation, we can observe the value of the roots in the graph of the function, however, when there is no graph, we can use the Bhaskara's formula to discover your values.

When the function has no roots, just use the formulas given at the beginning of this article to find the coordinatesofvertex.

Example

Which coordinates of vertex gives occupation: f(x) = x² – 12x + 20?

Solution: Like this occupation has roots, the coordinates of its vertex can be found by means of the method of the roots. However, we will use the following formulas:

x_v = - B
2nd

x_v = – (– 12)
2

x_v = 12
2

x_v = 6

y_v = - (B² – 4·a·c)
4th

y_v = – ([– 12]² – 4·1·[20])
4

y_v = – (144 – 80)
4

y_v = – (64)
4

y_v = – 16