Prisms are three-dimensional figures formed by two congruent and parallel bases, the bases, in turn, are formed by convex polygons. The other faces that are named side faces are formed by parallelograms. To determine the area of a prism, it is necessary to perform its planning and then calculate the area of the flat figure.
Read too: Differences between flat and spatial figures
Planning a prism
The idea of planning is to transform a three-dimensional figure into a two-dimensional figure. In practice it would be the equivalent of cutting over the edges of the prism. Below is an example of planning a triangular prism.

The same process can be adopted for every prism, however, note that as we increase the number of sides of the base polygons, the task becomes increasingly difficult. For this reason, we will make generalizations based on the planning of this polygon.
Calculation of the lateral area
Observing the image of the triangular prism, the parallelograms ABFC, ABFD and ACDE are the side faces.
Note that the side faces of a prism will always be parallelograms regardless of the number of sides of the base polygons, this happens because they are parallel and congruent.Looking at the triangular prism figure, we also see that we have three lateral faces. This is because of the number of sides of the base polygon, that is, if the prism bases are a quadrilateral, we will have four side faces, if the bases are a pentagon, we will have five side faces, and so on. Thus: the number of sides of the base polygon affects the number of side faces of the prism.
Therefore, the side area (AL) of any prism is given by the area of a side face multiplied by the number of side faces, that is, it is the area of the parallelogram multiplied by the number of sides of the face.
THEL = (base · height) · number of sides of face
Example
Calculate the lateral area of a regular hexagonal prism with a base edge equal to 3 cm and a height equal to 11 cm.
The prism in question is represented by:

The side area is then calculated by the area of the rectangle times the number of sides of the base polygon, which is 6, so:
THEL = (base · height) · number of sides of face
THEL = (3 · 11) · 6
THEL = 198 cm2
Calculation of base area

THE base area (THEB) of a prism depends on the polygon that composes it. As in a prism we have two parallel and congruent faces, the base area is given by the sum of the areas of the parallel polygons, that is, twice the area of the polygon.
THEB = 2 · polygon area
Read too:Flat Figure Areas
Example
Calculate the base area of a regular hexagonal prism with base edge equal to 3 cm and height equal to 11 cm.

The base of this prism is a regular hexagon, and this one, seen from above, looks like:
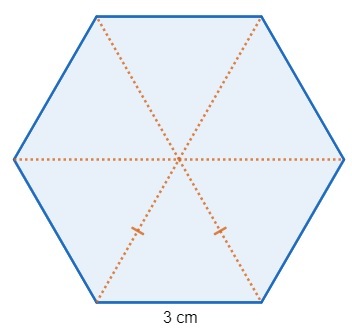
Note that the triangles formed inside the hexagon are equilateral, so the area of the hexagon is given by six times the equilateral triangle area.
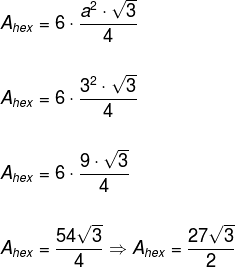
However, notice that, in the prism, we have two hexagons, so the base area is twice the area of the polygon.

Calculation of the total area
THE total area (AT) of a prism is given by the sum of the lateral area (THEL) with the base area (THEB).
THET = AL + AB
Example
Calculate the total area of a regular hexagonal prism with base edge equal to 3 cm and height equal to 11 cm.
From the previous examples, we have that AL = 198 cm2 and theB = 27√3 cm2. Therefore, the total area is given by:
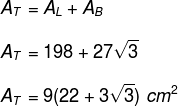
solved exercises
question 1 – A shed is shaped like a prism that is based on a trapeze, as shown in the figure.
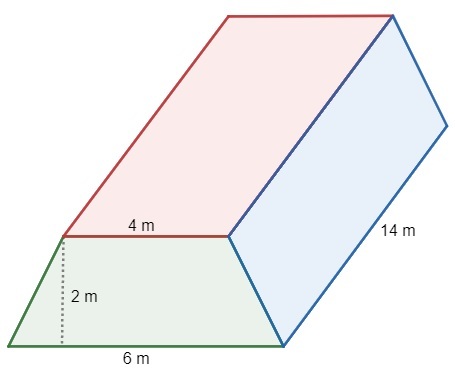
You want to paint this shed and it is known that the price of paint is 20 reais per square meter. How much will it cost to paint this shed? (Given: √2 = 1.4)
Solution
Initially, let's determine the area of the shed. Its base is a trapeze, so:
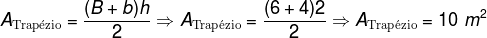
Therefore, the base area is:
THEB = 2 ·Atrapeze
THEB = 2 ·10
THEB = 20 m2
The side area in red is a rectangle, and we have the bottom, so this area is:
THEV = 2 · 4· 14
THEV= 112 m2
The area in blue is also a rectangle, but we don't have its base. Using the Pythagorean theorem in the triangle formed by the trapezoid, we have:
x2 = 22 + 22
x2 = 8
x = 2√2
So the rectangle area in blue is:
THETHE = 2 ·14·2√2
THETHE = 54√2 m2
Therefore, the lateral area of the prism is equal to:
THEL = 112 + 54√2
THEL = 112 + 75,6
THEL = 187.6 m2
And so the total area of this prism is:
THET= 20 + 187,6
THET= 207.6 m2
As the price of paint is 20 reais per square meter, the amount spent to paint the shed is:
20 ·207.6 = 4,152 reais
Reply: The amount spent to paint the shed is R$ 4,152.00
by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/calculo-area-um-prisma.htm
