You polygons are geometric figures bidimonthly formed by straight segments. Among the elements of polygons are vertices, sides and diagonals. At diagonals of a polygon are line segments that connect two of its non-consecutive vertices. The following images show the diagonals of some polygons in black:

Note that the number ofdiagonals increases when we also increase the number of sides of the polygon. The triangle has zero diagonals, the square has two, the pentagon has five, and the hexagon has nine.
Find a relationship between the number in diagonals on one polygon and its number of sides is no easy task, as it doesn't seem to exist. However, this relationship exists and depends on the number of diagonals that depart from a singlevertex of the polygon.
Diagonals starting from a single vertex
In the image below, see the amount of diagonals starting from vertex A of the polygons highlighted:
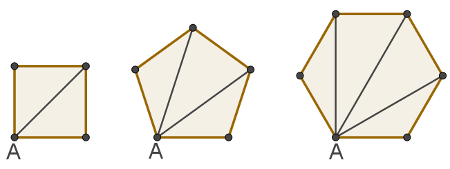
From the square comes a diagonal of vertex A. From the pentagon, two, and from the hexagon, three diagonals. The following image shows the diagonals starting from vertex A of a decagon.

Note that this geometric figure has ten sides and from each vertex there are seven diagonals. See below a table listing the number of sides of the figure and the number of diagonals starting from a samevertex (dv):

Note that the number of diagonalsleaving on one samevertex is always equal to the number of sides of the polygon minus three units. Thus, if the side of the polygon is represented by the letter n, we will have:
dv = n – 3
Total number of diagonals in a polygon
O total number ofdiagonals (d) of the polygon can be obtained from the following expression:
d = n (n - 3)
2
In other words, the number of diagonals of a polygon is always the product of the number of sides and the number of diagonals departing from the same vertex divided by two. This relationship applies to everyone convex polygon, that is, it has no recesses.
Examples
1st Example – What is the number of diagonals of a polygon that has 40 sides? How many diagonals depart from each vertex of this polygon?
Solution: It is not necessary to draw the figure to answer questions like these. To find the result of the first question, do:
d = n (n - 3)
2
d = 40(40 – 3)
2
d = 40(37)
2
d = 1480
2
d = 740
From the same vertex:
dv = n – 3
dv = 40 – 3
dv = 37
So there are 740 diagonals in total and 37 diagonals starting from the same vertex.
2ºExample – What is the number of sides of a polygon that has 25 diagonals starting from each vertex?
Solution:
dv = n – 3
25 = n – 3
n = 25 + 3
n = 28
There are 28 sides.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-diagonais-dos-poligonos.htm
