You Geometric solids they are figures that have three dimensions: height, width and length. Examples of geometric solids are: o cone, O paving stone, O cylinder it's the prism.
Although geometric solids are figures that cannot be defined in a single plane, they can be flattened. THE planning it is a way of representing these figures in just two dimensions.
A cardboard box, for example, is an object with three dimensions. But if we dismantle the box, we get its planning:
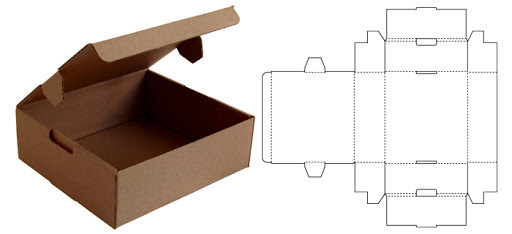
The planning of a geometric solid can have several uses, the main one is the calculation of the areafrom the surface of the solid. Let's see the flatness of some geometric solids.
Cone planning
O cone is a spatial geometric figure formed by straight line segments that start from a circle to a common point.
The flattening of a cone results in two flat geometric figures, one circle and a circular sector.


Planning the cobblestone
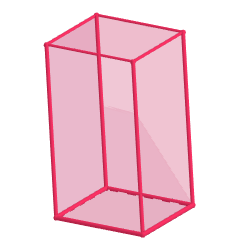
O paving stone is a particular case of a prism whose bases and faces are square, rectangular or diamond-shaped.
- Free Online Inclusive Education Course
- Free Online Children's Learning and Toy Library Course
- Free Online Math Games Course in Early Childhood Education
- Free Online Pedagogical Cultural Workshops Course
With the parallelepiped planning, we obtain six parallelograms, each one of them being one of its faces.
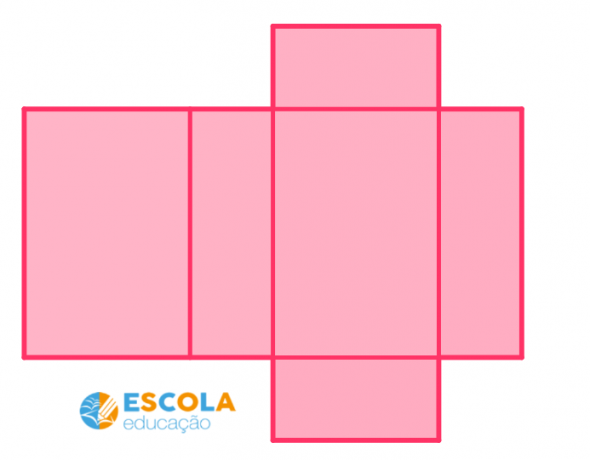
Cylinder Planning
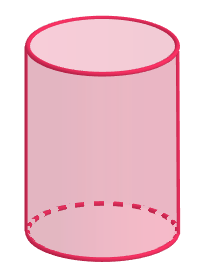
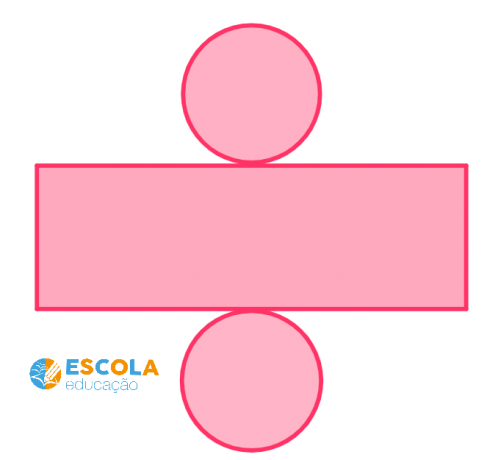
O cylinder it is a solid with a round and elongated body. It is formed by two circles, an upper and a lower, which are parallel, of the same size, and on different planes.
The figures resulting from the flattening of the cylinder are two circles and a parallelogram, which can be a rectangle, for example.
prism planning
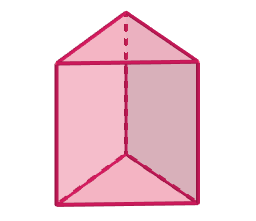
O prism is a spatial figure formed by two bases, which are congruent polygons and are located in distinct parallel planes. These bases can be triangles, squares, pentagons, hexagons, etc. The other faces of a prism are quadrilateral and are called side faces.
Next, we have the planning of a prism with triangular bases. In this planning, the plane figures obtained are two. triangles and three parallelograms.

You may also be interested:
- Area and perimeter
- Arithmetic average
The password has been sent to your email.
