Sum of internal and external angles of a convex polygon

You convex polygons are those that have no concavity. To see whether a polygon is convex or not, we must observe whether any straight line segment with ends in the figure does not pass through the outer region.

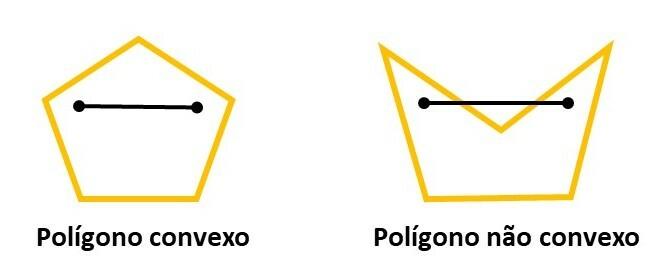
In convex polygons, there are formulas that allow you to determine the sum of the internal and external angles. Check out!

Sum of the internal angles of a convex polygon

The formula of sum of the internal angles of a convex polygon with n sides is:

$\dpi{120} \mathbf{S_i = (n-2)\cdot 180^{\circ}}$

Demonstration:

If we look, we will see that every convex polygon can be divided into a certain number of triangles. See some examples:

So, remembering that the sum of the inner angles of a triangle is always equal to 180°, we can see that the sum of the internal angles in these figures above will be given by the number of triangles that the figure could be divided times 180°:

quadrangle: 2 triangles ⇒ $\dpi{120} \mathrm{S_i = 2\cdot 180^{\circ} = 360^{\circ}}$
Pentagon: 3 triangles ⇒ $\dpi{120} \mathrm{S_i = 3\cdot 180^{\circ} = 540^{\circ}}$
Hexagon: 4 triangles ⇒ $\dpi{120} \mathrm{S_i = 4\cdot 180^{\circ} = 720^{\circ}}$

So to get a formula for calculating the sum of the interior angles of a convex polygon, we just need to know, generally speaking, how many triangles a convex polygon can be divided into.

instagram story viewer

If we observe, there is a relationship between this quantity and the number of sides of the figures. The number of triangles is equal to the number of sides of the figure minus 2, that is:

$\dpi{120} \mathrm{Total \, of \, tri\hat{a}angles =n - 2}$

Quadrilateral: 4 sides ⇒ n – 2 = 4 – 2 = 2
Pentagon: 5 sides ⇒ n – 2 = 5 – 2 = 3
Hexagon: 6 sides ⇒ n – 2 = 6 – 2 = 4

So, in general, the sum of the internal angles of a convex polygon is given by: $\dpi{120} \mathrm{S_i = (n-2)\cdot 180^{\circ} }$

Which is the formula we wanted to demonstrate.

Example:

Find the sum of the interior angles of a convex icosagon.

An icosagon is a 20-sided polygon, that is, n = 20. Let's replace this value in the formula:

$\dpi{120} \mathrm{S_i = (n-2)\cdot 180^{\circ} }$

$\dpi{120} \mathrm{S_i = (20-2)\cdot 180^{\circ} }$

$\dpi{120} \mathrm{S_i = 18\cdot 180^{\circ} }$

$\dpi{120} \mathrm{S_i = 3240^{\circ} }$

Therefore, the sum of the internal angles of a convex icosagon is equal to 3240°.

Sum of outside angles of a polygon

THE sum of the outside angles of a convex polygon is always equal to 360°, that is:

$\dpi{120} \mathbf{S_e = 360^{\circ}}$

Demonstration:

Check out some free courses

Free Online Inclusive Education Course
Free Online Children's Learning and Toy Library Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

We will demonstrate with examples that the sum of the outside angles of a convex polygon does not depend on the number of sides of the figure and is always equal to 360°.

Quadrilateral:

quadrangle Note that each inner angle forms a 180° angle with the outer angle. So, since there are four vertices, the sum of all angles is given by 4. 180° = 720°.

I.e: $\dpi{120} \mathrm{S_i + S_e = 720^{\circ}}$

Soon:

$\dpi{120} \mathrm{ S_e = 720^{\circ} - S_i}$

Once $\dpi{120} \mathrm{S_i = 360^{\circ}}$ , then:

$\dpi{120} \mathrm{ S_e = 720^{\circ} - 360^{\circ} = 360^{\circ} }$

Pentagon:

In the pentagon, we have 5 vertices, so the sum of all angles is given by 5. 180° = 900°. Soon: $\dpi{120} \mathrm{S_i + S_e = 900^{\circ}}$ . Then: $\dpi{120} \mathrm{ S_e = 900^{\circ} - S_i}$ . Once $\dpi{120} \mathrm{S_i = 540^{\circ}}$ , then: $\dpi{120} \mathrm{ S_e = 900^{\circ} - 540^{\circ} = 360^{\circ} }$ .

Hexagon:

In the hexagon, we have 6 vertices, so the sum of all angles is given by 6. 180° = 1080°. Soon: $\dpi{120} \mathrm{S_i + S_e = 1080^{\circ}}$ . Then: $\dpi{120} \mathrm{ S_e = 1080^{\circ} - S_i}$ . Once $\dpi{120} \mathrm{S_i = 710^{\circ}}$ , then: $\dpi{120} \mathrm{ S_e = 1080^{\circ} - 720^{\circ} = 360^{\circ} }$ .