StrengthWeight of a body is the strengthgravitational, uniquely attractive, produced by a second massive body, like the Earth, the Moon or the Sun, for example. According to the law of universal gravitation, two bodies that contain mass attract each other with a force inversely proportional to the square of the distance separating them.
Force weight, gravitational force or simply weight are fundamentally the same thing, however it is quite common for us to confuse the concepts of weight and mass, which are different. While weight is a force, measured in newtons (N), the mass of a body is the amount of matter it contains, measured in kilograms (kg).
Also access: mass x weight
What is weight in physics?
Weight is strength that arises from attractiongravitational between two bodies consisting of mass, knowing this, we can calculate it by multiplication between the pasta of one of these bodies, measured in kilograms, and the acceleration of the gravity location, in m/s². while our mass remains invariant when we move between two points with different severities, ourWeightchanges.
Per example: a 10 kg object on Earth, where gravity is approximately 9.8 m/s², will have a weight of 98 N, while on the Moon, where gravity is 1.6 m/s², the weight of this body would be of only 16 N.

Lookalso:Understand why we don't feel the Earth rotate
weight strength formula
The formula used to calculate weight strength is this, check it out:
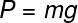
P - weight (N)
m - mass (kg)
g - local gravity (m/s²)
O Weight, because it is a strength, é vector. This force always points towards the center of the Earth and is responsible for keeping us stuck on its surface. Similarly, the Sun draws the Earth towards its center, that is, this star exerts a heavy force on our planet.
THE why the earth does not fall towards the sun is the great speed at which our planet orbits around the star. Furthermore, because it is a force that always points to the center of the Earth's trajectory around the Sun, the force gravitational effect that it does on that one is not able to affect the modulus of the translational velocity, only its sense.
Do not stop now... There's more after the advertising ;)
Weight and Newton's Third Law
According to the Newton's third law, when we exert a force against a body, we receive back from it the same force, in the same intensity and direction, but with the opposite direction. Applied in the context of weight, this law indicates that the force the Earth puts on us downwards is applied to the Earth upwards, and that is correct. If the Earth is able to pull us towards its center, we also exert a force on it of the same intensity, but in the opposite direction.
The reason we fall towards the Earth, and not the other way around, is the inertia: the Earth's mass is much larger than our masses, so its tendency to remain at rest is much greater, so that the acceleration acquired by it, thanks to the weight force we exert, is negligible, almost nil.
readalso:What would happen if the Earth stopped rotating?
normal weight and strength
Normal force and strength and weight are often confused as an action and reaction pair. However, these forces act on the same body and, therefore, violate the condition established by thirdlawinNewton. In fact, the normal force is a compression reaction force which is made on some surface, not by force weight.
strength work weight
The work performed by a force measures the amount of energy that has been transferred between two or more bodies. The formula that is used to calculate the work of the weight force is this, check it out:

τ - work (J - joule)
P - weight (N - newton)
d - displacement (m - meter)
θ - angle between strength and weight
The formula shows us that the amount of work done by the weight force depends on the intensity of that force multiplied by the displacement, but also on the angle θ, formed between displacement and weight force. Let's check out some special cases:
When angle θ is equal to 0º: If the weight force and displacement form an angle of 0 degrees, the weight force will be positive, that is, the work of the weight force will produce an increase in kinetic energy, as when an object falls towards the center of the Earth.
When angle θ equals 180º: In this case, the weight force and displacement are opposite, as when we throw an object upwards, here on Earth: when we do, the body loses kinetic energy, since the work is negative, as the cosine of 180° is equivalent to 1.
When angle θ equals 90º: Since the cosine of 90° is 0, the weight force will not do work in directions perpendicular to it, such as when walking horizontally. In this case, the body's weight will not produce any change in its kinetic energy.
See too: Check out what's most important about Newton's three laws
force weight and gravitation
THE gravitationuniversal is one of Newton's laws, this law states that all bodies endowed with mass attract each other in pairs, with the same force. Furthermore, this law indicates that the attractive force between bodies is proportionalto theproductinyourpastas and inverselyproportionalthe distance between them squared. Check out the universal gravitation formula:

FG - gravitational force (N)
G - universal gravitation constant (6.674.10-11 N.m²/kg²)
M and m - body masses (kg)
r - distance between bodies (m)
The first formula shown on the left is what we call the law of universal gravitation, in it, you can see that, in addition to mass m, there is the term GM/r², this term is used to calculate the accelerationgivesgravity produced by a body of mass M, at a point at a distance r from its center of mass. Also, the letter G is a proportionality constant that applies to all bodies.
Through the formula on the right, shown in the previous figure, it is possible to calculate the gravity of the Earth on its surface. For this, we will make use of the Earth's mass (M = 5.972.1024 kg), the equatorial radius of the Earth (r = 6.371.106 m) and the gravitation constant (G = 6.674.10-11 N.m²/kg²), and thus we will be able to estimate the gravity of the Earth on its surface:

The result shows that Isaac Newton's theory of universal gravitation is able to predict the magnitude of the Earth's gravity, and its results are compatible with those measured by the most accurate instruments.

See too:Why doesn't the Moon fall to Earth?
Weight Strength Exercises
Question 1) Regarding the concepts of weight and mass, check the INCORRECT alternative:
a) Weight is calculated by the mass of the body multiplied by the acceleration of local gravity.
b) Weight and mass are different physical quantities.
c) The weight force points downward.
d) Weight is a vector quantity, measured in newtons.
e) Mass is a scalar quantity measured in kilograms.
Template: Letter C
Resolution:
The only incorrect statement is the letter C, it says that the weight points down, which is wrong. Since the weight force is a vector quantity, its definition depends on a frame of reference. For us, for example, a person on the other side of the globe has his weight pointing upwards. It would be correct to say that the weight always points towards the center of the Earth.
Question 2) On the Moon, where gravity is equal to 1.6 m/s², a person's weight is 80 N. On Earth, where gravity is 9.8 m/s², this person's mass, in kg, will be equal to:
a) 490.0 kg
b) 50.0 kg
c) 8.2 kg
d) 784.0 kg
e) 128 kg
Template: Letter B
Resolution:
First we must calculate the person's mass based on their weight and gravity on the Moon, check:

From the above calculations, we find that the mass of this body is equal to 50 kg, however, we ask for the mass of the body on Earth, which must be equal to its mass elsewhere. Thus, the correct alternative is the letter B.
Question 3) An object has a weight of 2231 N on the surface of Jupiter, where gravity is 24.79 m/s². What should the weight of this body be on Mars, where gravity is 3.7 m/s²?
a) 333 N
b) 90 N
c) 900 N
d) 370 N
e) 221 N
Template: Letter a
Resolution:
Based on the mass and weight of the body on Jupiter, we can calculate its mass on Mars, see:

After we have discovered the body mass (90 kg), we apply the weight formula again, this time using Mars gravity (3.7 m/s²). Thus, we find that the weight of this body on Mars must be 333 N.
By Me. Rafael Helerbrock