O Thales' theorem was developed by the mathematician Thales of Miletus, who demonstrated the existence of a proportionality in the straight segments formed by parallel lines cut by transversal lines.
From this theorem, it is possible to see proportionality relations in various situations, which has wide application, such as astronomy and triangles. Miletus Tales he was a pre-Socratic philosopher who made great contributions not only to philosophy, but also to mathematics, in his quest to better understand the Universe.
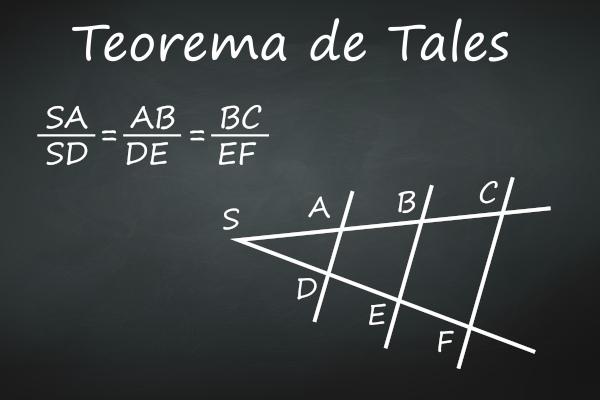
Statement of Thales' Theorem
Thales' theorem states that:
A bundle of parallel lines determines proportional segments on two transversal lines.
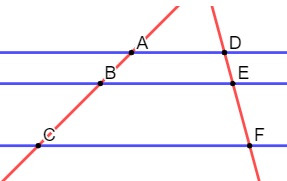
In the image, there are several line segments: AB, BC, DE, EF, AC, DF. You can compare them in two ways. One is to compare the segments of the same transversal line:
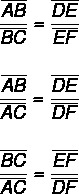
Another way to carry out this comparison, but which still generates the same result, is to assemble the ratio between the segment of a transverse straight line under the equivalent segment.
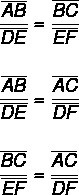
Regardless of the shape chosen to assemble the proportions, it is possible to find the value of these segments from the fundamental property of the proportion.
See too: Length measurements - units of measurement and conversion
Do not stop now... There's more after the advertising ;)
How to apply Thales' theorem
In practice, Thales' theorem is used in order to find unknown values in situations involving parallel lines and transverse lines.
Example:
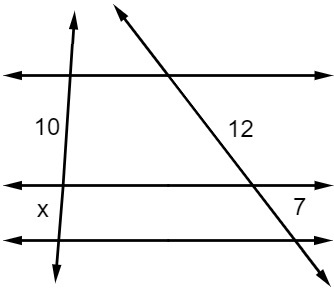
assembling the proportion, we have that 10 is to x, as 12 is to 7, that is:
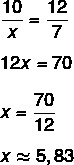
Thales' theorem in triangles
One of the most important applications of Thales' theorem is in the study of triangles. To the draw a line parallel to the base, it is possible to build a triangle smaller similar to the larger triangle. In addition, the segments formed by the side of the triangle are also proportional, which makes it possible to apply Thales' Theorem to find unknown values in this triangle.
Example:
Calculate the value of BD knowing that the line segment DE is parallel to the base of the triangle AC.
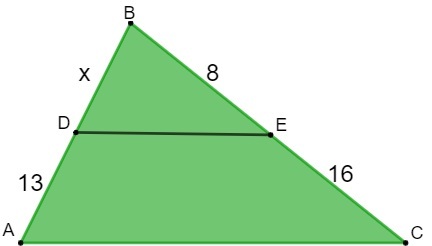
Assembling the ratio, we know that x is to 13, just as 8 is to 16.
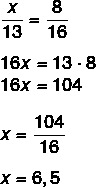
Read too: Triangle classification - criteria and nomenclature
solved exercises
Question 1 - (Fuvest) Three plots of land face street A and street B, as shown in the figure. The side borders are perpendicular to street A. What is the measure of x, y, and z in meters knowing that the total front for this street is 180 m?

A) 90, 60 and 30
B) 40, 60 and 90
C) 80, 60 and 40
D) 20, 30 and 40
Resolution
Alternative C.
We know that the sum of x + y + z = 180 m.
Adding the sides of street A, we have: 40 + 30 + 20 = 90 m.
Assembling the proportions to find the value of x, we have:
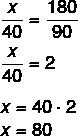
Therefore, x = 80 meters. Now we'll find the value of y:
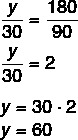
Since y = 60 meters, we can then find the value of z:

Question 2 - (IFG) Let the triangle ABC in the figure below be measured as follows: AC = 50 cm, AE = 20 cm, and AD = 10 cm.
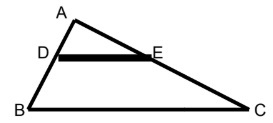
Knowing that DE is parallel to BC, the measure of side AB is de?
A) 15 cm
B) 20 cm
C) 25 cm
D) 30 cm
E) 35 cm
Resolution
Alternative C.
Since DE is parallel to BC, we can apply Thales' theorem.
Data: AC = 50 cm, AE = 20 cm and AD = 10 cm.
We know that AC is to AE as AD is to AB.

By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Theorem of Thales"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/teorema-tales.htm. Accessed on June 27, 2021.



