Polyhedra are spatial geometric shapes that have all flat faces. They are considered spatial because they have three dimensions (length, width and height). These spatial forms are present in the world around us. A laundry detergent box, for example, is a polyhedron called a cobblestone. The die, which is part of many games and games, is also a polyhedron, called a cube. These objects are studied by mathematics through geometry. They have characteristics and properties that are very important for your understanding.
Let's get to know the elements of a polyhedron.
As mentioned before, polyhedra are spatial geometric shapes that have flat faces. But what are the faces of a polyhedron?
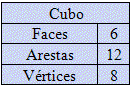
Imagine a dice. Each quantity represented on the die is on one “side” of that object. Each “side” of the die is called a face. Thus, we can say that the data has six faces.

The face is one of the elements of any polyhedron. The other elements are: edges and vertices. Let's understand what these other two elements are.
Edges are the lines resulting from the meeting of two faces. That is, when two faces meet they form a line and this line is called an edge.
The cube has 12 edges.
Vertices are the meeting points of edges. That is, edges of a polyhedron meet at a point and that point is the vertex of the polyhedron.
From the figure we can see that the cube has 8 vertices.
We can make a small table with the cube elements:
Let's determine how many faces, how many edges and how many vertices the polyhedron below has.
This polyhedron is a pyramid. About it, we can say that:

Now, let's see if you are able to complete the table for the following polyhedron:

By Marcelo Rigonatto
Mathematical
Kids School Team

