O trapeze is a picture of plane geometry very present in our daily lives. Its about a polygon that has four sides, being two parallel sides (known as base major and base minor) and two non-parallel (oblique sides). Like every quadrilateral, it has two diagonals, and the sum of its internal angles is always equal to 360º.
A trapeze can be classified as rectangle trapeze, when it has two right angles; isosceles trapeze, when the non-parallel sides are congruent, that is, they have the same measure; and scalene trapeze, when all sides have different measurements. The perimeter of a trapezoid is calculated by adding up its sides, and there are specific formulas for calculating the area and Euler median of the trapezoid.

Elements of a trapeze
We define as whole trapeze quadrilateral which has two parallel sides. The parallel sides are known as base major and base minor. Like every quadrilateral, it has two diagonals, and the sum of the internal angles is equal to 360º.
The elements of the trapeze are:
Four sides;
Two sides parallel to each other and two not parallel;
Four vertices;
Four internal angles, whose sum equals 360º;
Two diagonals.
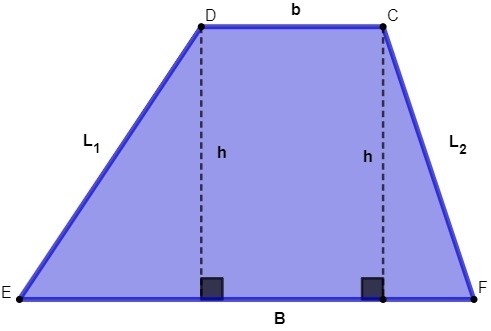
C, D, E, F: vertices
B: major trapeze base
B: lower base of the trapeze
H: height
L1 and L2: oblique sides
Read too:Circle and circumferences - flat figures that can raise doubts
trapeze classification
There are three possible classifications for a trapeze according to its shape. A trapezoid can be rectangle, isosceles, or scalene.
Do not stop now... There's more after the advertising ;)
rectangle trapeze
It has two angles straight.
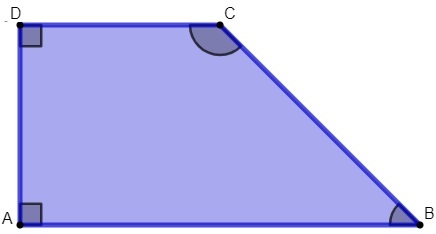
isosceles trapeze
It has congruent oblique sides, that is, non-parallel sides have the same measurement.

Scalene Trapeze
It has all distinct sides.

Trapezium Properties
As a specific property of the trapeze, we can state that the adjacent angles of non-parallel sides have sum equal to 180º.

a + d = 180º
b + c = 180º
Specific properties for the isosceles trapeze
There are two properties that are specific to the isosceles trapeze. The first one is that the base angles, as well as the non-parallel sides, are congruent.

The second property of the isosceles trapeze is that when we plot the heights, we form two triangles congruent, in addition to being possible to apply the Pythagorean theorem in that triangle.
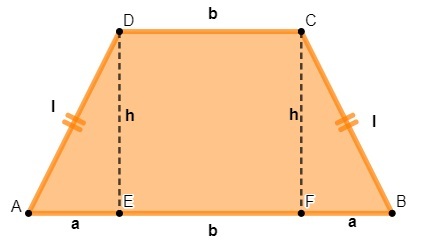

Observation: There is a relationship in the larger base – it is not a property, but it is an important relationship for solving exercises – which we can describe as:
B = b + 2a
See too: Equilateral triangle - properties and particularities
Perimeter of the trapeze
The perimeter of any trapezoid is calculated by adding all sides.
P = B + b + L1 + L2
Example
What will be the amount of wire, in meters, to make five turns in the terrain that has the shape of the scalene trapeze below:

Resolution
P = 18 + 13 + 7 + 9 = 47 meters.
Since there will be five laps, then 5P = 5. 47 = 235 meters of wire.
trapeze area
To calculate the trapeze area, there is a specific formula, which depends on the value of the bases and the height.
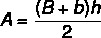
Example
In a glass shop, the glasses are produced to order, costing R$ 96.00 per m². To build the glass that will sit on a table in the shape of a trapeze (largest base measures 1.3 m; smaller base measures 0.7 m; height measures 1 m.), the amount spent on the glass will be?
Resolution
B = 1.3
b = 0.7
h =1

As the table is exactly 1 m², R$ 96.00 will be spent.
Middle base of the trapeze
The middle base of the trapezius is the segment parallel to the base major and base minor that joins the midpoints of the oblique sides.

AND and F they are midpoints of their respective sides, and the segment formed by connecting these points is the base midpoint. The length of the average base is calculated by the arithmetic mean between the largest base and the smallest base:

Trapezius median
Known as Euler's median of the trapezius (Mand), it is about the straight segment formed by the connection between the midpoints of the two diagonals of the trapeze.

To calculate the Euler median length, the formula is as follows:

Example1
Find the length of the median of the trapezius whose bases measure 7 cm and 10 cm.
Resolution

Example 2
Calculate the value of the major base and minor base of the trapezoid below knowing that M and N are midpoints of the diagonals.

Resolution
We know that B = 2x + 7, b = 3x -1 and Mand = 2, therefore:

Since x = 4, then it is possible to find the largest base and the smallest base by substituting x.

Also access: Point, Line, Plane and Space: Basic Concepts of Geometry
Exercises solved
Question 1 - Knowing that a trapezoid has a base greater than 15 and a base less than 7, the value of the difference between the length of its average base and its Euler median is equal to?
a) 11
b) 4
c) 6
d) 7
e) 8
Resolution
1st step: calculate the average base length.

2nd step: calculate the length of the Euler median.

3rd step: calculate the difference between Bm inand.
11 – 4 = 7
Therefore, the correct alternative is the letter “d”.
Question 2 - The bases of an isosceles trapezius measure 6 cm and 14 cm, and an oblique side measures 5 cm, so it can be said that the area of this trapezius, in cm², is:
a) 28
b) 30
c) 32
d) 34
e) 40
Resolution
To calculate the area of this trapeze, we need to find the height. For this, we will draw an isosceles trapeze with the information given:
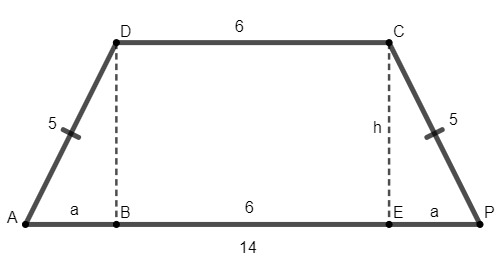
How to calculate the area we need the value of the two bases and the value of H, which we don't know yet, let's find the value of The to apply the Pythagorean theorem to the CEP triangle.
We know that:

Finding the value of The, it is possible to calculate the value of h by the Pythagorean theorem.

Knowing the value of h, it is possible to calculate the trapezium area:
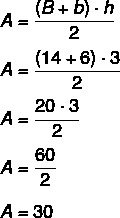
Therefore, the correct alternative is the letter “b”.
By Raul Rodrigues de Oliveira
Maths teacher