Consider the polynomial equation below where all coefficients Thenoare integers:
Thenoxno + then-1xn-1 + then-2xn-2 + … + the2x2 + the1x + a0 = 0
O Rational Roots Theorem guarantees that if this equation admits the rational number P/what as root (with P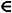
, what 
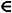
and mdc (p, q) = 1), then The0 is divisible by P and Theno is divisible by what.
Comments:
1º) The rational roots theorem does not guarantee that the polynomial equation has roots, but if they do exist, the theorem allows us to identify all roots of the equation;
2º) if Theno= 1 and the other coefficients are all integers, the equation has only integer roots.
3°) if q = 1 and there are rational roots, these are whole and divisors of The0.
Application of the Rational Roots Theorem:
Let's use the theorem to find all the roots of the polynomial equation 2x4 + 5x3 – 11x2 – 20x + 12 = 0.
First, let's identify the possible rational roots of this equation, that is, the roots of the form P/what. According to the theorem, The0 is divisible by P; in this way, how
The0 = 12, then the possible values of P are {±1, ±2, ±3, ±4, ±6, ±12}. Analogously, we have to Theno is divisible by what and Theno = 2, then what can have the following values: {±1, ±2}. Therefore, dividing the values of P per what, we get possible values P/what roots of the equation: {+½, – ½, +1, – 1, +3/2, –3/2, +2, –2, +3, –3, +4, –4, +6, –6, +12, –12}.To confirm that the values we found are really the root of the polynomial equation, let's substitute each value in place of the x of the equation. Through algebraic calculus, if the polynomial results in zero, so the substituted number is actually the root of the equation.
2x4 + 5x3 – 11x2 – 20x + 12 = 0
For x = + ½
2.(½)4 + 5.(½)3 – 11.(½)2 – 20.(½) + 12 = 0
For x = – ½
2.(– ½)4 + 5.(– ½)3 – 11.(– ½)2 – 20.(– ½) + 12 = 75/4
Do not stop now... There's more after the advertising ;)
For x = + 1
2.14 + 5.13 – 11.12 – 20.1 + 12 = – 12
For x = – 1
2.(– 1)4 + 5.(– 1)3 – 11.(– 1)2 – 20.(– 1) + 12 = 18
For x = + 3/2
2.(3/2)4 + 5.(3/2)3 – 11.(3/2)2 – 20.(3/2) + 12 = – 63/4
For x = - 3/2
2.(– 3/2)4 + 5.(– 3/2)3 – 11.(– 3/2)2 – 20.(– 3/2) + 12 = 21/2
For x = + 2
2.24 + 5.23 – 11.22 – 20.2 + 12 = 0
For x = – 2
2.(– 2)4 + 5.(– 2)3 – 11.(– 2)2 – 20.(– 2) + 12 = 0
For x = + 3
2.34 + 5.33 – 11.32 – 20.3 + 12 = 150
For x = – 3
2.(– 3)4 + 5.(– 3)3 – 11.(– 3)2 – 20.(– 3) + 12 = 0
For x = + 4
2.44 + 5.43 – 11.42 – 20.4 + 12 = 588
For x = – 4
2.(– 4)4 + 5.(– 4)3 – 11.(– 4)2 – 20.(– 4) + 12 = 108
For x = + 6
2.64 + 5.63 – 11.62 – 20.6 + 12 = 3168
For x = – 6
2.(– 6)4 + 5.(– 6)3 – 11.(– 6)2 – 20.(– 6) + 12 = 1248
For x = + 12
2.124 + 5.123 – 11.122 – 20.12 + 12 = 48300
For x = – 12
2.(– 12)4 + 5.(– 12)3 – 11.(– 12)2 – 20.(– 12) + 12 = 31500
Therefore, the roots of the polynomial equation 2x4 + 5x3 – 11x2 – 20x + 12 = 0 they are {– 3, – 2, ½, 2}. Through polynomial decomposition theorem, we could write this equation as (x + 3).(x + 2).(x – ½).(x – 2)= 0.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Rational Roots Theorem"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/teorema-das-raizes-racionais.htm. Accessed on June 28, 2021.
