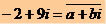The applications of mathematical definitions are essential in physical studies, because through calculations we obtain evidence for theories related to Physics. The trigonometric functions sine, cosine and tangent are present in several branches of Physics, helping in calculations related to Kinematics, Dynamics, Optics, among others. In this way, Mathematics and Physics walk together with the sole objective of providing knowledge and expanding new scientific research. See through solved examples the applications of Mathematics in Physics.
Example 1 - Dynamics
Formula that allows you to calculate the work of force F on the displacement d of a body:
τ = F * d * cos Ө
Determine the work done by the force F of intensity √3/3 over a 2m path, as shown in the illustration, assuming that the surface is smooth. Use 30º cosine = √3/2.


Example 2 - Kinematics: Oblique Launch
The maximum height reached, the ascent time and the horizontal reach are some of the elements that constitute an oblique throw. According to the angle formed between the launch and the surface, the body can travel different trajectories. If the slope (angle) increases, the object logically reaches a higher height and a smaller horizontal reach; if the tilt angle decreases, the height also decreases and the horizontal reach becomes greater.
Do not stop now... There's more after the advertising ;)

An object is launched obliquely into vacuum with an initial velocity of 100m/s with an inclination of 30°. Determine the rise time, maximum height and horizontal reach of the object. Consider g = 10m/s².
rise time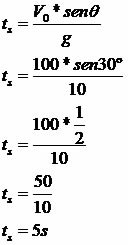
Maximum height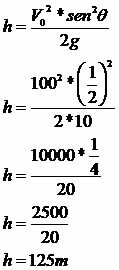
horizontal reach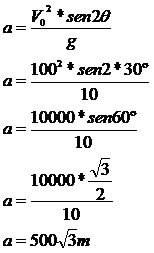
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Trigonometric Applications in Physics"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/aplicacoes-trigonometricas-na-fisica.htm. Accessed on June 27, 2021.