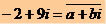The polynomial-type algebraic equation is expressed as follows:
P(x) = Thenoxno +... + the2x2 + the1x1 + the0
i.e
P(x) = 2x5 + 4x4 + 6x3 + 7x2 + 2x + 9
Every polynomial has a coefficient and a literal part, the coefficient being the number and the literal part the variable.
The polynomial is made up of monomials and each monomium is formed by the product of a number with a variable. See below the structure of a monomium:
Monomial
The1. x1 → the1 = coefficient
→x1 = literal part
Every polynomial has degree, the degree of a polynomial in relation to the variable will be the largest value of the exponent referring to the literal part. The dominant coefficient is the numerical value that accompanies the higher degree literal part.
To identify the degree of a variable, we can use two methods:
The first considers the general degree of the polynomial and the second considers the degree in relation to a variable.
To get the general degree of the polynomial, we must consider that each monomium of the polynomial has its degree, which is given by the sum of the exponents of the terms that make up the literal part. See the example:
2xy + 1x3 + 1xy4 → Polynomial
2xy → Degree 2 monomium, since the variable x has an exponent of 1 and the variable y has an exponent of 1, when adding the exponents referring to the variables, we have the degree of this monomium is 2.
1x3→ Monomium of grade 3, because the variable x has the exponent 3.
1xy4 → Monomium of degree 5, since variable x has degree 1 and variable y has degree 4, when adding the exponents referring to the variables we have to the degree of this monomium is 5.
O general degree of the polynomial will be given by the highest degree monomium, hence the degree of the polynomial 2xy + 1x3 + 1xy4 é 5.
To get the degree of a polynomial in relation to a variable, we must consider that the degree will be obtained through the largest exponent of the variable that will be fixed. Suppose this variable is the x term of the polynomial 2xy + 1x3 + 1xy4, We have to:
2xy → monomium of degree 1, since the degree of this algebraic term is being determined by the exponent of the variable x.
1x3→ Monomium of degree 3, since the degree of this algebraic term is being determined by the exponent of the variable x.
xy4→ Monomium of degree 1, since the degree of this algebraic term is being determined by the exponent of the variable x.
the degree of the polynomial 2xy + 1x3 + 1xy4é 3, as it is the greatest degree of the polynomial in relation to the variable x.
Take a look at the example below to understand how we obtain the degree of a polynomial through these two procedures:
Example 1
Given the 5x polynomial8 + 10y3x6 + 2xy. What is the degree of the polynomial related to the variable x and what is its dominant coefficient? What is the degree of the polynomial in relation to variable y and what is its dominant coefficient? What is the general degree of the polynomial?
Reply
First step:You should find the degree of the polynomial related to the variable x. We then have to apply the second case to find the degree of the polynomial 5x8+ 10y3x6+ 2xy.
Do not stop now... There's more after the advertising ;)
First we must consider each monomium separately and evaluate the degree through the variable x.
5x8→ In relation to variable x, the degree of this monomium is 8.
10y3x6 → In relation to variable x, the degree of this monomium is 6
2xy → With respect to variable x, the degree of this monomium is 1.
So we have that the highest degree of the 5x polynomial8 + 10y3x6 + 2xy, related to variable x, is 8 and its dominant coefficient is 5.
Second step: Now let's find the degree of polynomial 5x8 + 10y3x6 + 2xy, in relation to the variable y. It follows the same structure as the previous step for identification, only now we must consider it in relation to variable y.
5x8 = 5x8y0→ With respect to variable y, the degree of this monomium is 0.
10y3x6→ With respect to variable y, the degree is 3.
2xy → With respect to variable y, the degree is 1.
We have then that the degree of the polynomial related to variable y is 3 and its dominant coefficient is 10.
Third step: We must now identify the general degree of the polynomial 5x8 + 10y3x6+ 2x, for this we consider each monomium separately and add the exponents referring to the literal part. The degree of the polynomial will be the degree of the largest monomial.
5x8 = 5x8y0→ 8 + 0 = 8. The degree of this monomium is 8.
10y3x6 → 3 + 6 = 9.The degree of this monomium is 9.
2xy → 1 + 1 = 2. The degree of this monomium is 2.
So we have that the degree of this polynomial is 8.
The concept referring to the degree of a polynomial is fundamental for us to understand what a unitary polynomial.
By definition, we have to: O unitary polynomial it happens when the coefficient that accompanies the highest degree literal part in relation to a variable is 1. This degree is given by the monomium Thenoxno, Where Theno is the dominant coefficient that will always be equal to 1 and the degree of the polynomialIt is given by xno,which will always be the largest exponent of the polynomial in relation to a variable.
Unitary Polynomial
P(x) = 1xno +... + the2x2 + the1x1 + the0
Being theno =1 and xno it is the literal part that has the highest degree of the polynomial.
Note throughout unitary polynomial we always evaluate the degree in relation to a variable.
Example 2
Identify the degree of unit polynomials below:
The) P(x) = x3 + 2x2 + 1 B) P(y) = 2y6 + y5 – 16 ç) P(z) = z9
Reply
The) P(x) = 1x3+ 2x2 + 1. The degree of this polynomial must be obtained in relation to the variable x. The highest degree in relation to this variable is 3 and its coefficient is 1, considered as the dominant coefficient. Hence, the polynomial P(x) is unitary.
B) P(y) = 2y6 + y5 – 16. The degree of this polynomial with respect to variable y is 6. The coefficient that accompanies the literal part referring to this degree is 2, this coefficient being different from 1, so the polynomial is not considered unitary.
ç) P(z) = z9. The degree is 9 and the coefficient in relation to the highest degree of the variable z is 1. Therefore, this polynomial is unitary.
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Naysa Crystine Nogueira. "Unit polynomial"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/polinomio-unitario.htm. Accessed on June 29, 2021.
Learn the definition of polynomial equation, define a polynomial function, the numerical value of a polynomial, the root or zero of the polynomial, Degree of a polynomial.