Some flat regions resemble polygons known as triangle, square, rectangle, rhombus, parallelogram, trapeze, pentagon, hexagon, among others, where each one has a specific formula to determine the area of its surface. But some regions have formats not defined by Mathematics, they are irregular shapes. In this case, we need to try to decompose the figure into known parts, individually calculating the area of each one, which will be added together to constitute the total area of the region. Note the area of an irregular region:

Decomposition of the area into known figures:

The region area consists of a rectangle, a triangle and a trapezoid. Now we just need to determine the areas of each figure.
Area 1 - Rectangle
The rectangle referring to area 1 has the following dimensions:

Its area is calculated by multiplying the length by the width:
A = 24 * 12
A = 288 m²
Area 2 - Triangle
Do not stop now... There's more after the advertising ;)
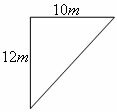
The area of a triangular region is calculated by half multiplying the base by the height.
A = (10*12) / 2
A = 120/2
A = 60 m²
Area 3 - Trapeze

The area of a trapeze is given by the following expression:  , Where:
, Where:
B: larger base
b: smaller base
h: height
Then:

The total area of the region is given by the sum of the areas of regions 1, 2 and 3:
Total area = 288m² + 60m² + 88m²
Total area = 436 m²
Any irregular region can be decomposed into simpler figures, however, in some situations, the calculation can be a little more complex. For such situations, the area of the region is determined through integrals (content related to higher education).
by Mark Noah
Graduated in Mathematics
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Area of a Flat Region"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/area-uma-regiao-plana.htm. Accessed on June 28, 2021.