The set of complex numbers is formed by all z numbers that can be written in the following form:
z = a + bi
In this form, i = √(– 1). In these numbers, a is called real part and b is called imaginary part. To represent the numberscomplexes geometrically, we will use vectors on the plan.
Geometric representation of complex numbers
You numberscomplexes can be represented geometrically in a flat built similarly to Cartesian plane: two perpendicular axes which, in turn, are number lines. Furthermore, these two lines are found at its origins.
The difference between this plan and the flatCartesian it's just the interpretation: the x-axis of this plane is called the real axis, and the y axis is called the imaginary axis. So, to represent a complex number in this plane, known as plan of Argand-Gauss, we must turn this number into an ordered pair, where the x coordinate is the partreal of the complex number and the y coordinate is yours. partimaginary.
After that, the vector that represents a numbercomplex
is always the straight segment oriented that starts at the origin of the plan of Argand-Gauss and ends at point (a, b), where a is a partreal of the complex number and b is its imaginary part.In other words, the biggest difference between these plans is that, in flatCartesian, we score points and, in the plan of Argand-Gauss, we use the real and imaginary part of complex numbers to mark vectors.
The following image shows the representationgeometric of numbercomplex z = 2 + 3i.
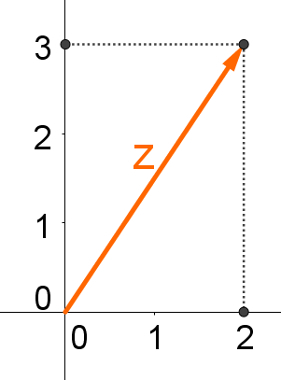
Geometric representation of complex number addition
Given the complexes z = a + bi and u = c + di, we have the following algebraic addition:
Do not stop now... There's more after the advertising ;)
a + u = a + bi + c + di
a + u = a + c + (b + d) i
Note that from the point of view geometric, what is done when adding numberscomplexes is the sum of their coordinates on the same axis.
Geometrically, the sum between the complexes z = a + bi and u = c + di can be done as follows:
1 – Draw vectors z and u in the plane of Argand-Gauss;
2 – Download a copy of the vector u for the endpoint of vector z. In other words, draw a vector the same length as vector u and parallel to it from point (a, b).
3 – Download a z’ copy of vector z for the endpoint of vector u;
4 – Note that the vectors u, u’, z and z’ form a parallelogram, and construct a vector v that starts from the origin and ends at the meeting between the vectors u’ and z’.
5 - v = z + u
Note this construction in the image below:

O vector v is just the diagonal of this parallelogram formed by the vectors u, u’, z and z’.
Example
Consider vector a = 1 + 7i and vector b = 3 – 2i. See the construction of the parallelogram from these two vectors:
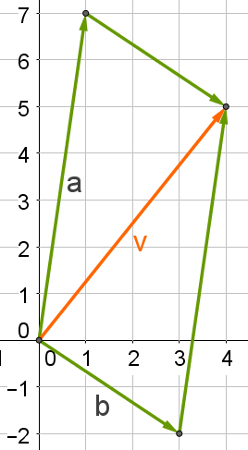
Thus, it is possible to determine the result of the sum between these two vectors observing the coordinates of the vector v = (4, 5). Therefore, the complex number v = 4 + 5i.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Geometric representation of the sum of complex numbers"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/representacao-geometrica-soma-numeros-complexos.htm. Accessed on June 28, 2021.

