THE association of electric generators concerns how these devices are connected to a electric circuit. Depending on the need, it is possible to associate the generators in series or in parallel. At Associationinseries generators, add up the electromotive forces individual generators, as well as their electrical resistances internal, in the case that these generators are real.
Read too: 5 Things You Should Know About Electricity
Concept
The association of generators in series ensures that we can provide a greater electromotive force than only a generator would be able to offer an electrical circuit. For example: if a circuit operates under an electrical voltage of 4.5 V, and we only have 1.5 V batteries, it is possible to connect them in series so that we apply a potential of 4.5 V on this circuit.
A simple and didactic example involving the association of generators in series is the lemon battery experiment. In this one we connect several lemons in series so that the electrical potential produced by the fruits is large enough to turn on a small light bulb.

When paired in series, lemons can be used to light a lamp.
In the association of generators in series, all generators are connected on the same branch of the circuit, and for that reason, everyone will be crossed by the same electric current. THE electromotive force total offered to the circuit is determined by the sum of the electromotive forces of each of the generators.
Despite being very useful for many applications, connecting real generators in series implies a increased electrical resistance of the circuit, and, therefore, a greater amount of energy will be dissipated in the form of heat, through the joule effect.
See too: The speed of electric current
Do not stop now... There's more after the advertising ;)
Important formulas
According to the characteristic equation of generators, the electromotive force (ε) represents all the energy that a generator can produce. However, part of this energy is dissipated (r.i) by the generators' own internal resistance. In this way, the energy that is supplied by the circuit is given by the useful voltage (U):

Uu — Useful voltage (V)
ε — electromotive force (V)
ri — internal resistance (Ω)
i — electric current (A)
When we connect generators in series, we just add their electromotive forces as well as the potentials dissipated by their internal resistances. By doing this, we find the pouillet's law. According to this law, the intensity of the electric current produced by an association of n generators can be calculated based on the following expression:
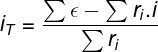
Σε — Sum of electromotive forces (V)
Σri —sum of the internal resistances of the generators (Ω)
iT — total circuit current (A)
Analyzing the previous expression, we can see that it allows us to calculate the electric current that is formed in the circuit. To do so, she relates the sum of electromotive forces divided by the sum of internal resistances. However, the law shown is only applied to the association of generators in series, if there are resistors external to the association of generators. The electrical current of the circuit can be calculated using the following formula:
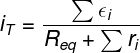
Req — Equivalent circuit resistance (Ω)
An example of this situation is shown in the following figure. In it we have two generators (batteries) connected in series that are connected to two electrical resistances (lamps), also connected in series.

In the figure we have two generators associated in series connected to two lamps, also connected in series.
Summary
When associating generators in series, all generators are connected to the same branch (wire).
In this type of association, all generators are traversed by the same electrical current.
When connected in series, the electromotive force of the association of generators is given by the sum of the individual electromotive forces.
The equivalent resistance of the association of generators in series is given by the sum of the individual resistances.
In series association, the electromotive force supplied to the circuit increases. However, the amount of energy dissipated by the Joule effect also grows.
Check out some solved exercises on the association of generators in series below and understand more about the subject.
See too:Physics formula tricks
solved exercises
Question 1) Two real generators, as shown in the following figure, with electromotive forces equal to 10 V and 6 V, respectively, and internal resistances of 1 Ω each, are associated in series and connected to a resistor of 10 Ω. Calculate the electrical current that passes through this resistor.

a) 12.5 A
b) 2.50 A
c) 1.33 A
d) 2.67 A
e) 3.45 A
Template: Letter C
Resolution:
Let's calculate the total electrical current in the circuit. For this, we will use Pouillet's law for generators connected in series:

In the calculation made, we added the electromotive forces produced by each of the generators (10 V and 6 V) and divided this value by the modulus of the equivalent resistance of the circuit (10 Ω) with the sum of the internal resistances (1 Ω) of the generators. Thus, we find an electrical current of 1.33 A.
Question 2) Three identical generators, of 15 V each and 0.5 interna of internal resistance, are connected in series to a set of 3 resistors of 30 Ω each, connected in parallel to each other. Determine the strength of the electrical current formed in the circuit.
a) 2.8 A
b) 3.9 A
c) 1.7 A
d) 6.1 A
e) 4.6 A
Template: Letter B
Resolution:
To solve this exercise, it is necessary to first determine the modulus of the equivalent resistance of the three external resistors. As these three 30 Ω resistors are connected in parallel, the equivalent resistance of this connection will be 10 Ω:

Once this is done, we can move on to the next step, in which we add the electrical potentials of each generator and divide the result by the sum of the equivalent and internal resistance:

When we apply the values in Pouillet's law, we find an electric current with an intensity equal to 3.9 A. Therefore, the correct alternative is the letter B.
Question 3) Two identical batteries of 1.5 V each and internal resistance of 0.1 Ω are associated in series with a lamp of resistance equal to 10.0 Ω. The electrical current that passes through the lamp and the electrical voltage between its terminals are, respectively, equal to:
a) 0.350 A and 2.50 V
b) 0.436 A and 4.36 V
c) 0.450 A and 4.50 V
d) 0.300 A and 5.0 V
e) 0.125 A and 1.25 V
Template: Letter B
Resolution:
Through Pouillet's law, we can find the module of the electric current that passes through the lamp, observe:
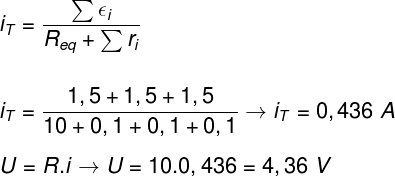
The calculation made allows us to determine that the electrical current that passes through the lamp is 0.436 A and that the electrical potential between its terminals is 4.36 V. The result is consistent with the energy balance of the exercise, as together the three batteries can deliver a maximum of 4.5 V.
By Me. Rafael Helerbrock